２次関数の解の存在範囲と対数の融合問題

猫が徘徊する数学ランドへようこそ☆

今回は、２次関数の解の存在範囲についての入試問題を丁寧に解説します。

それではさっそく問題を見ていきましょう。

黄色チャート『２次関数の解の存在範囲』の練習問題に対数をまぜて、ちょっとだけ難しくした、というレベルですね。

aは定数でa＞1とする. xの２次方程式　\(x^2－2a^tx＋a＝0\)　が aより小さい２つの異なる実数解を持つような実数tの値の範囲を求めよ.
題材：東京海洋大学(2017年)海洋工学部	難易度：★★★☆☆☆☆☆☆☆

まずは、\(f(x)＝x^2－2a^tx＋a\)と置いて探っていきましょう。

\(f(x)＝0\)の解が、aより小さい２つの異なる実数解を持つ条件を、以下に３つ列挙します。

ひとつめ

解の判別式の値が０より大きい‥‥① これは、２次関数とｘ軸との交点が２つあるための条件です。 この条件を満たさないと、そもそも交点が２つ存在しないことになってしまいますよね。

ふたつめ

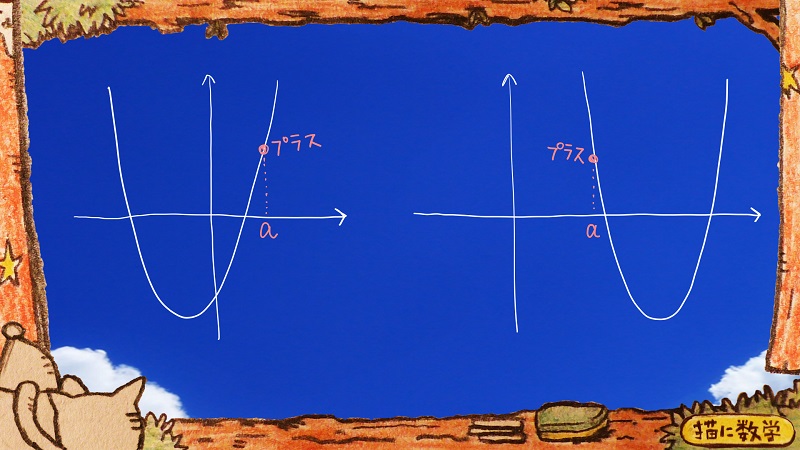
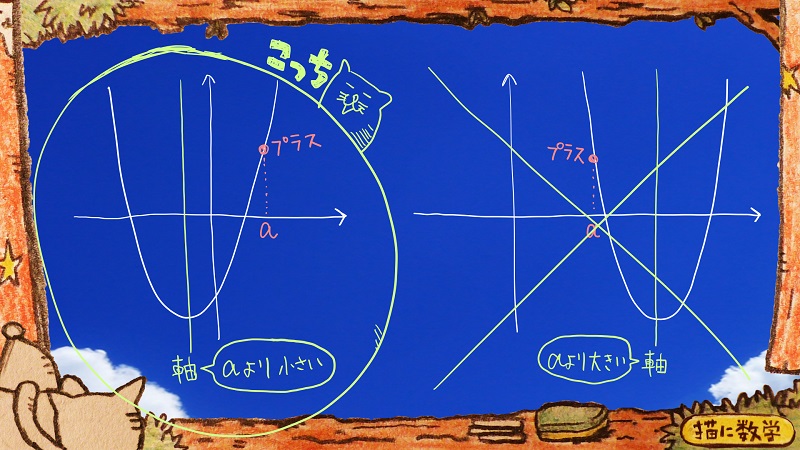
\(f(a)\)の値が０より大きい‥‥② 『\(f(x)＝0\)の解が、aより小さい２つの異なる実数解を持つ』ということは、 ２次関数のグラフとｘ軸との２つの交点がx＝aよりも左側に存在しなければいけません。 その状況を想像してみると、x＝aのときのグラフの高さは、プラスの領域になければならないことになります。 ただこの条件だけだと、次の二つの状況が想定されるので、ここでもう一つの条件を登場させて、さらに限定します。

みっつめ

二次関数の軸のx座標の値がaより小さい‥‥③ この条件を加えることで ２次関数のグラフとｘ軸との２つの交点がx＝aよりも左側に存在してくれることになります。

以上、３つの条件を満たすためのｔの範囲を探っていくことになります。

２次関数の解の存在範囲からｔの範囲を探す

解の判別式の値が０より大きい‥‥①

まずはこれですが、解の判別式をDとすると

\(\frac{D}{4}＝(a^t)^t－a＞0\)となります。

よって

\(a^{2t}＞a\)

a＞1というのが問題文に条件としてありましたので

指数同士の大小関係はそのまま

\(2t＞1\)となります。

ゆえに

\(t＞\frac{1}{2}\)

これが①の条件より導き出されたｔの範囲です。

次に③の条件を探ります。

二次関数の軸のx座標の値がaより小さい‥‥③

二次関数の式を平方完成させて頂点のｘ座標を求めます。

ちなみに、公式 \(ax^2＋bx＋c＝0\)の二次関数の頂点のｘ座標は \(\frac{－b}{2a}\)である。 を使っても容易に求められます。 参考講座▶裏技！簡単に二次関数の頂点の座標を求める３つの方法と小技テクニック

平方完成させると

\(f(x)＝(x－a^t)^2＋a－a^{2t}\)となり、

この二次関数の頂点のｘ座標は

\(a^t\)となります。

これがaより小さいので

\(a^t＜a\)

となり、ゆえに

t＜1

が③より導き出されたｔの範囲となります。

\(f(a)\)の値が０より大きい‥‥②

まず、\(f(a)\)＞0を表現します。

\(f(a)＝a^2－2a^t \cdot a＋a＞0\)

a＞0(つまり、aはゼロでなくて、なおかつ正の符号)なので、

不等号の向きは変わらずaで割ることができます。

したがって不等式の両辺をaで割るとこのようになります。

\(a－2a^t＋1＞0\)

これを変形して

\(a^t＜\frac{a＋1}{2}\)

a＞1なので

両辺のaを底とする対数をとると、不等号の向きは変わらず

\(\log_aa^t＜\log_a\frac{a＋1}{2}\)

となって

\(t＜\log_a\frac{a＋1}{2}\)

となります。これが②の条件より導き出されたｔの範囲です。

ｔの範囲の絞り込み

さて、３つの条件からｔの範囲の条件がこのように導き出されました。

\(t＞\frac{1}{2}\)

t＜1

\(t＜\log_a\frac{a＋1}{2}\)

これらにすべて共通するｔの範囲が求めるｔの範囲ということになります。

お気付きの通り、ややこしいのが

\(t＜\log_a\frac{a＋1}{2}\)ですね。

つまり、ここで

\(\frac{1}{2}\)と1と\(\log_a\frac{a＋1}{2}\) の大小関係を求めよ。

という問題を解く必要がある、ということですね。

その手順はこちら↓に詳しく解説しています。

関連講座▶対数の大小比較の練習問題

結局これは

\(\frac{1}{2}＜\log_a\frac{a＋1}{2}＜1\)ということになって

ｔの範囲をそえぞれ数直線上で書き記すと、このような状況になりました。

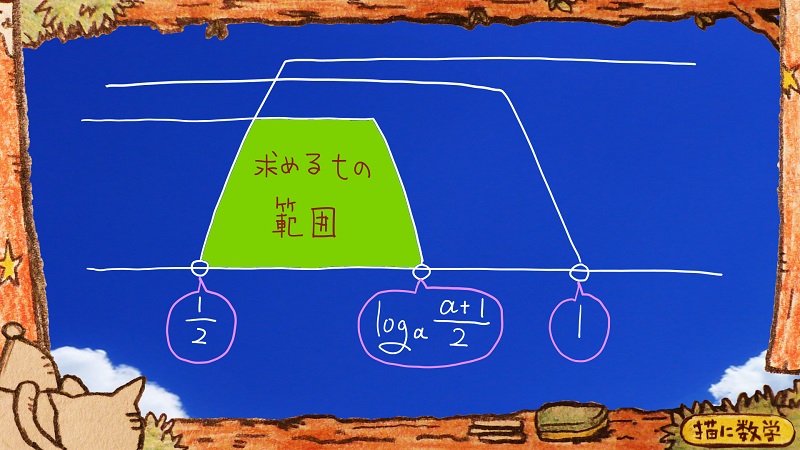
\(t＞\frac{1}{2}\)

t＜1

\(t＜\log_a\frac{a＋1}{2}\)

なので、この共通範囲を求めて

\(\frac{1}{2}＜t＜\log_a\frac{a＋1}{2}\)

が求めるｔの範囲ということになりました。

以上、今回は二次関数の解の存在範囲と対数が登場する基本レベルの問題を解説しました★