二次関数の頂点の座標を求め方～裏技、小技テクニック

今回は、二次関数の頂点の座標を求める方法（裏技というか小技テクニック）をご紹介します。

前回は、あたえられた二次方程式を平方完成することによって、頂点の座標をもとめる練習をしました。

平方完成の方法とコツについて練習問題プリント付きで解説

今回は、平方完成をしないで、二次関数の頂点の座標を求める方法を解説していきます。

やり方は二つあって、ご覧のように、すでに頂点のｘ座標を文字で表現したものを当てはめるという方法と、因数分解によって求める方法とがあります。

つまり、全部で３通りの方法があるわけですね☆

それでは解説していきます。

まず一つ目の方法ですが、

頂点のｘ座標である

\(－\frac{b}{2a}\)

を使います。

ちなみに頂点のｙ座標を表現している

ややこしいかたまりは使いません。

また、

\(－\frac{b}{2a}\)

と覚えてもいいですし、解の公式を暗記したときの最初に登場していた

（にーえーぶんのまいなすびー）の部分
\(\frac{－b}{2a}\)

を使っても値は同じになります。

これだと新たに暗記する労力はほぼ必要ないですよね。

使い方ですが、③の問題が理解しやすいので、これでちょっと具体的に見ていきましょう。

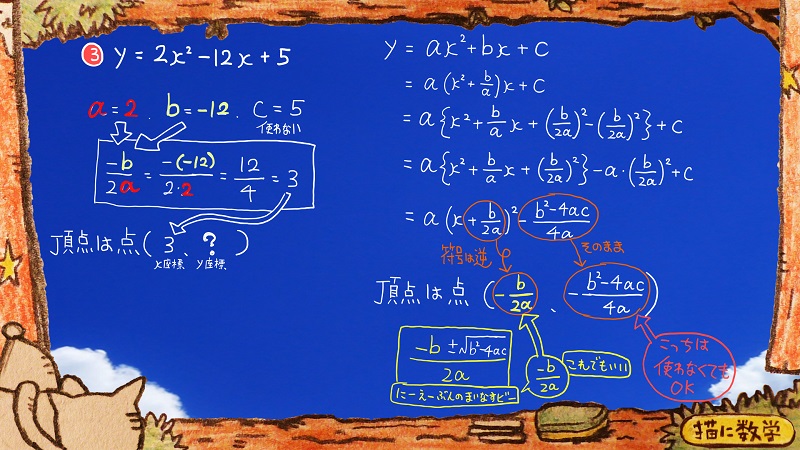
③の問題は

右辺にある式の各定数を比べると

a＝２

b＝－１２

となります。

cにあたるのは５なのですが、これは使いません。

\(\frac{－b}{2a}\)

にそれぞれ値を代入して計算すると

３という値になりました。

これがすなわちこの二次関数の頂点のｘ座標ということになります。

あとはその時のｙ座標を求めればOKですね。

頂点のｘ座標が３だとわかっているわけですから、「この二次関数のｘが３のときのｙの値を求めればいい」ということなので、この二次関数のｘに３を代入します。

するとｙ以外のすべての項が数字になってくれて、ｙの値が求められる、ということになります。

計算の結果、ｙの値が－１３

ということになりましたので

頂点のｘ座標が３のとき、その時のｙ座標は－３ということで、頂点の座標が明らかになりました。

この方法を使って、①から⑥までのすべての二次関数の頂点を求めるとこのようになります。

表の左から右側にむかって順に求めていくことになります。

平方完成の手順を必要としない場合は、この方法で求めてもいいでしょう。

次は因数分解を利用した方法を紹介します。

①の問題で説明します。

この二次関数の左辺であるｙに０を代入します。

それによって出来上がった二次方程式は

この関数のｙが０の時、ｘの値は何か？

を求める方程式ができあがったことになります。

つまり、①の二次関数をグラフにしたときに、グラフとｘ軸とが交わるポイントのｘ座標を求める方程式ができた、ということになります。

この二次方程式の右辺は因数分解することができます。

ｘ(ｘ－６)になりましたね。

ｘがゼロのときも、ｘ－６が０のときも、この方程式は成り立つわけですから、そのときのｘを求めると、

ｘは０または６

ということになります。

それをグラフに書き込むと、ご覧のようになります。

グラフとｘ軸との交点のｘ座標が０と６なのですから、そのちょうど間に頂点のｘ座標があるということはわかるかと思います。

もっと正確に言うなら、頂点のｘ座標の値は０と６の平均の値そのものである、と言うことができます。

なので０と６を足して２で割った値が、頂点のｘ座標になります。

計算すると３だということがわかったので、後は先程のやり方と同様、二次関数のｘに３を代入します。

これは、ｘが３の時のｙの値を求める手順になりますので、これを計算して、結局ｙ＝－９だということがわかりました。

この方法で、頂点のｘ座標とｙ座標を求める、という手もあります。

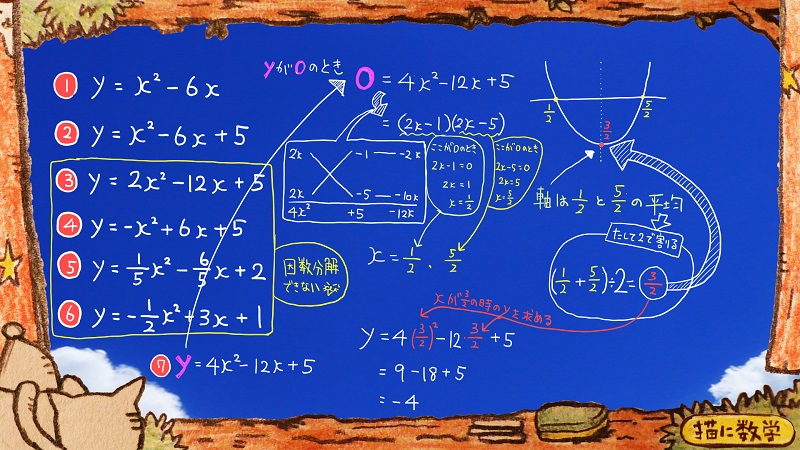
次の②の問題も同様に解いてみましょう。

まずｙに０を代入します。

出来上がった二次方程式はこの関数のグラフがｘ軸と交わるポイントのｘ座標を求めるものになっています。

右辺は因数分解できますね。

たして５

かけて－６になる

二組の数字は

－１と－５なので

それを因数分解された形にほうりこみます。

ｘ－１がゼロになるときも、ｘ－５がゼロになるときも

ともに方程式が成り立ちますので、

その時のｘをそれぞれ求めて、

ｘ＝１または５

ということになります。

この１と５の平均の値が、この二次関数のグラフの頂点のｘ座標の値になりますので

たして２で割ります。

３になりましたね。

あとは頂点のｘ座標である３を、もとの二次関数のｘに代入すると、ｘが３のときのｙの値が出てきてくれるというワケです。

どうでしょうか？

ちょっと慣れてきたかと思います。

最後に⑦を新たに登場させて終わりにしたいと思います。

というのも、③から⑥の問題は因数分解をすることが困難なので、この方法は適さないからです。

⑦の問題は、ご覧のように、たすきがけによる因数分解によってグラフとｘ軸との交点を求めることができます。

ただ、ここまで因数分解がややこしくなると、最初に紹介した

\(\frac{－b}{2a}\)

に代入して求めるほうがてっとり早いですね。

問題によっては、最初からグラフとｘ軸との交点が判明している時もあります。

その場合は、この発想で頂点を求めさせることも考えられますので、どちらにせよ知っておいてほしい考え方です。

以上、今回は平方完成を使わないで二次関数の頂点の座標を求める裏技（小技テクニック)を解説しました。

また、こちらも内容の近いものですので、二次関数の教科書レベルの基本をマスターしたい方はご覧いただいて理解を深めてください☆

平方完成をして頂点の座標を求める方法

二次関数と二次不等式の違いって？

ご覧いただいて、どうもありがとうございました☆