食塩水の濃度の難問を灘高校の数学で解説します

どうも坂田です☆

今回は食塩水の濃度を求める数学の難問を解説していきます。

灘高校の2017年に出題された数学の入試問題（過去問）です。

これから解説をしていきますので必要な方はここで画面をストップして解いてみてください。

それでは以下、解説に移ります。

問題文が長く、まずは事態を把握する必要があります。

特に、（操作）の内容を整理する必要がありそうですね。

三つの問いがありますが、とりあえず図を書いて、状況を把握してみることにします。

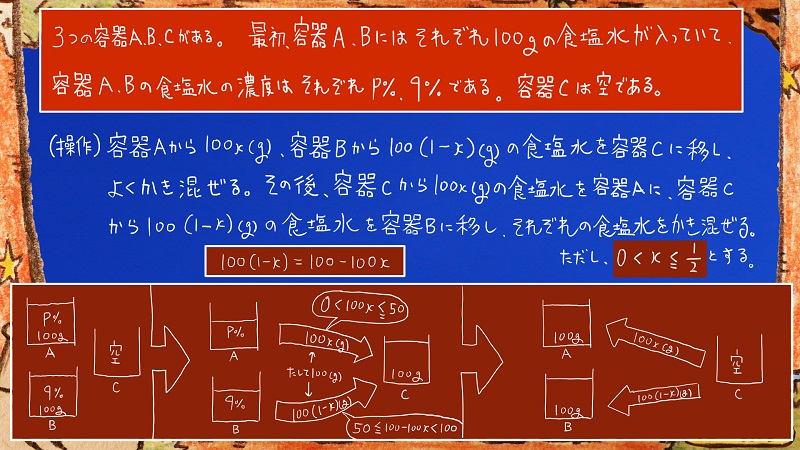
１回の操作で起こる変化の様子を、数式と図で整理してみました。

Aの容器からは濃度ｐパーセントの食塩水100ｘグラムが

Bの容器からは濃度ｑパーセントの食塩水100(1－x)グラムが

それぞれCの容器へと移動することになります。

ｘの値の範囲が

０より大きくて、２分の１以下

ということですので

容器AからCに移される100ｘグラムの範囲は

０グラムより大きくて、５０グラム以下

ということになります。

最大でも５０グラムまで、ということになりますね。

そして、容器Bから容器Cに移される食塩水の量

100(1－x)グラムというのがちょっとピンとこないかもしれません。

その場合、これを展開すると

100－100ｘグラムになりますね。

100ｘグラムは容器Aから容器Cに移される量でした。

なので、もしも

100ｘグラムが３０グラムだとしたら

100－100ｘグラムは７０グラムということになりますよね。

つまり、AとBの容器から、合計して１００グラムの食塩水が容器Cに移されるということになります。

そのあと、容器Cはかき混ぜられ、その濃度の食塩水が、容器Aと容器Bにそれぞれ１００グラムになるまで戻されます。

これが操作の内容です。

では、様子が把握できたところで１つ目の問題を見てみましょう。

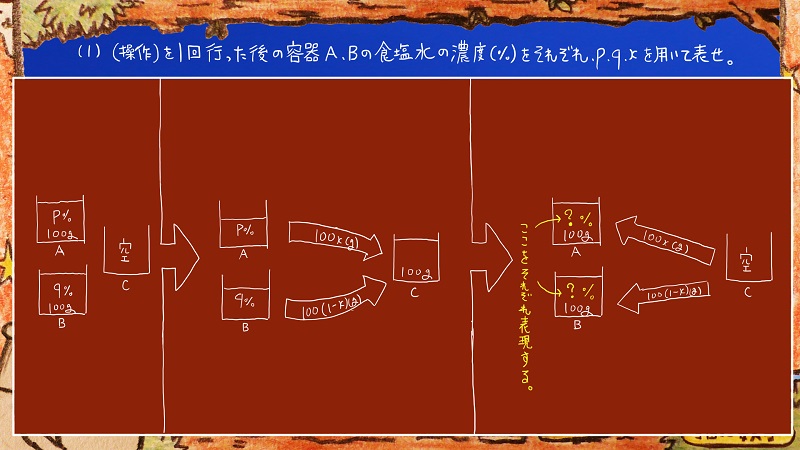
１問目は、操作を1回行った時の容器A、Bの食塩水の濃度をそれぞれｐ、ｑ、ｘを用いて表すという問題です。

黄色で表された部分の濃度をそれぞれ表現するということですね。

操作後の容器A、Bの食塩水は共に100グラムだということはわかっているのですから、あとはそこに含まれる食塩の量がわかればいいということになります。

それを求めるために、各工程の様子を追っていきましょう。

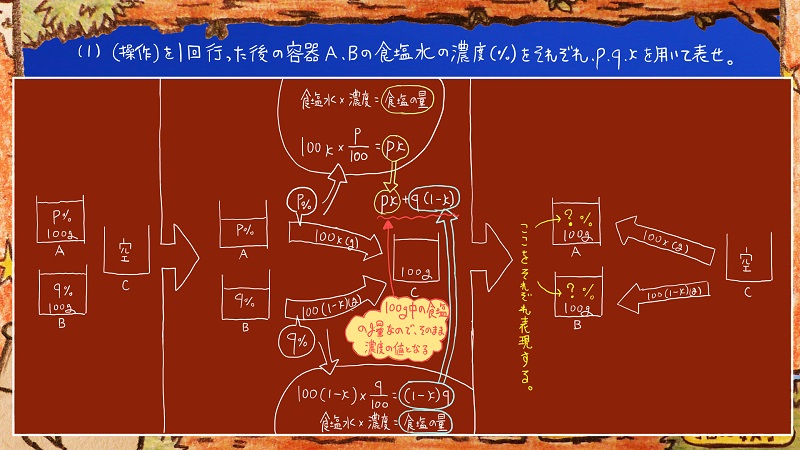
まず、容器Cに合計１００グラムの食塩水を移す工程を見ていきます。

容器Cは食塩水が１００グラムになるということはわかってるのですが、その濃度がわかりません。

濃度を求めるために、容器A、Bからそれぞれやってきた食塩の量を計算してみます。

まずは容器Aからやってきた食塩の量について計算します。

濃度ｐパーセントの１００ｘグラムの食塩水には

ｐｘグラムの食塩が含まれています。

次に、容器Bからやってきた食塩の量について計算すると

ｑ(１－ｘ)グラムということになります。

それらの合計が

容器Cの食塩水に含まれている食塩の量ということになります。

容器Cの食塩水は100グラムなので

グラムで表された食塩の量が

そのままパーセント表記の濃度ということになります。

つまり、容器Cには

ｐｘ＋ｑ(１－ｘ)　パーセント

の食塩水100グラムがあることになります。

では、これをもとに、１問目の答えを求めてみましょう。

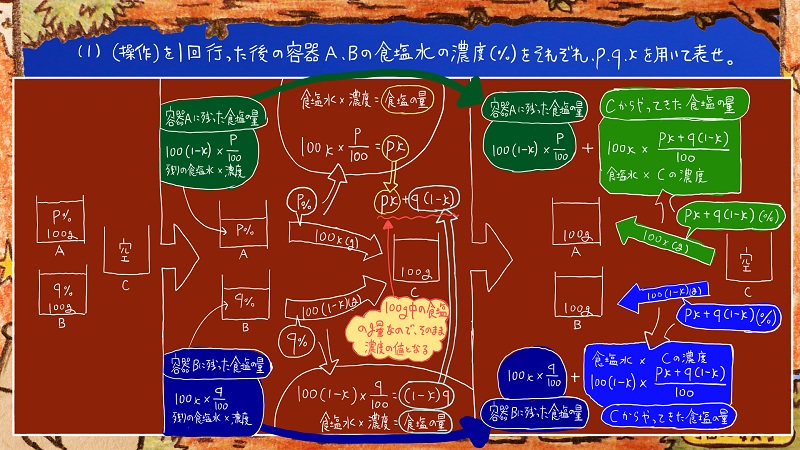
一番右のほうをご覧ください。

容器Cから容器A、Bに食塩水を戻す操作のところです。

この時にそれぞれ移動した食塩の量を計算した式が書いてあります。

また、それに加えて、容器A、Bに残っていた食塩水にあった食塩の量をそれぞれ計算して加えていますね。

容器Aには濃度ｐパーセントの食塩水100(1－x)グラムが残っていましたし

容器Bには濃度ｑパーセントの食塩水100xグラムが残っていました。

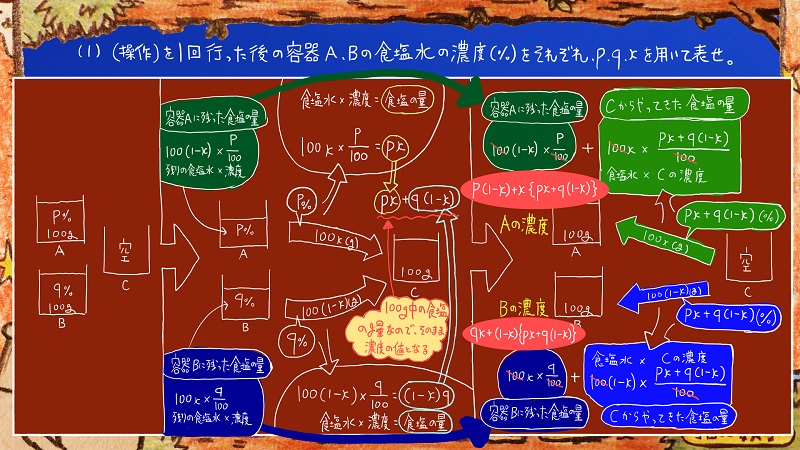
このようにして食塩の量をグラムでそれぞれ求めると、１００グラム中の食塩水に含まれる食塩の量が判明します。

そしてこれは、そのまま濃度（パーセント）の値としてみなすことができますよね。

よって容器A、Bの濃度はそれぞれこのようになります。

では次の問題を見てみましょう。

問題文の情報をまとめるとこのようになります。

ここで新たに加わった情報は、操作前の容器Bの食塩水の濃度と、操作後の容器Aの食塩水の濃度の値が明らかになったということです。

表を見ると、操作後の容器Aの濃度が二通りで表現できるということがわかります。

この部分を方程式で表現せよ、ということですね。

しかも、文字のｑは１０という数値を代入できるのでその方程式に含まれる文字は、ｐとｘのみになります。

このようになるわけですね。

ここで、文字ｘをなんとかして

ｘの２乗－ｘ＋１

という形をつくることで

この方程式を

ｐとｔだけで表現されたものにする、というのがこの問題の指示です。

ちょっとやってみましょう。

文字ｐに着目してくくり出すと

ｔのワンセットができました。

残ったｘの塊も同様にしたいので、ここは先にもうワンセット書いてしまって、つじつまを合わせるようにして表現を足していきます。

このように、ｔのセットをもうひとつ作ろうとしたら、－１０が必要だということがわかりました。

なので、

－１０と＋１０を書き足して

変形に破綻がないよう調節します。

これでｐとｔだけの表現に置き換えることができました。

では最後の問題を解いてみましょう。

（２）の問題の条件を引き継いで、２回目の操作が行われるという問題です。

操作を２回行う、という文面を読んだ時、とてもややこしく感じる方もいるかと思いますので、とりあえずその様子を観察してみましょう。

右下の茶色い２本の矢印の説明図を見てください。

まず、１回目の操作はこのように、すでに容器A、Bの濃度の変化の様子は数式で表現できていますね。

続いて２回目の操作ですが

このように

１回目の操作が完了したときの容器A、Bの濃度をそれぞれa、ｂと表現するなら、２回目の操作が完了したときも、同様な変化を見せてくれるということがわかるかと思います。

これをまとめたのが上の表になるのですが。

この表から、方程式をあと２つ作ることができます。

それがコレですね。

ここで重要なのは

ｔを求めてからそれを利用してｘを求めるのでは？

という（２）を利用するという発想です。

そもそもこの２つの方程式も、文字が複雑に踊りまくっていますので、シンプルな表現へ導くための誘導だったと考えると、この場合すんなり変形していけます。

（２）のときと同じ要領で

ｔで置き換えられる形へと変形させていきます。

真ん中の方程式は、ご覧のようになりました。

ここで右の方程式を観察してみると、真ん中の方程式と比べて、形といい、式を変形させていく操作の過程といい、まったく同じであることに気が付きます。

もしも真ん中の方程式と同様の操作で変形していった場合、ご覧のようにそれぞれの値が対応する形でｔの含む式が出てくることになります。

結局このように３つの方程式を用意することができました。

あとはこれを使って

ｐとｔを求めて、

さらにｔの値からｘを求めて完了です。

ここからはちょっと複雑な連立方程式になります。

解き方は１通りではありませんが

重要なポイントは『ｂはとりあえず必要ない』という点です。

なのでとりあえずｂを消去すれば、ドツボにハマることはありません。

この場合、②を③に代入してｂを消去してから

それに①を代入するとうまいこと解けるようになっています。

ここで紹介する手順は、

ｂを消去する前に、③に代入する式をシンプルにしてからｂを消去する方法になります。

まず、①と②の式を観察すると、左端の部分がかなりにていることがわかります。

①の式の一部に赤線が引いてありますが、その部分を変形すると

－ｔ(10－ｐ)の形になって

②の式に対して辺々を加えると

ｐ＋６＝ｂ

が出てきました。

これを③に代入して

ｂを消去します。

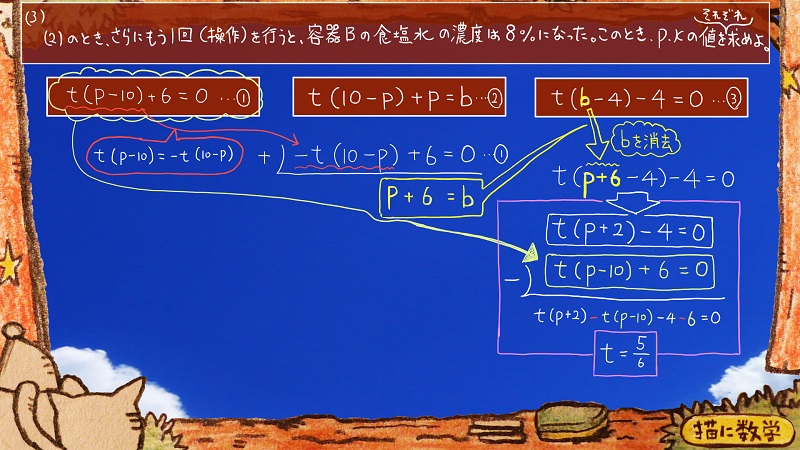
次に、その式と①で

辺々を引きます。

これを整理するとｔが求められました。

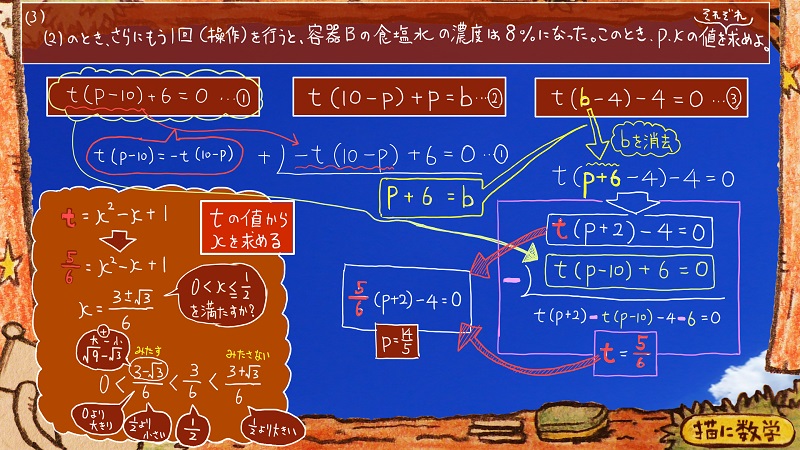
これによってｐも明らかになったので

あとはｔの値からｘを求めるという作業をすれば完了になります。

左下の囲みにそれが書いてありますが

ｔとｘの関係式から

ｘの値が二つ求まります。

ｘには範囲がありましたので、それを満たすかどうかの検証をします。

６分の３の分子のところにルート３を加えた数は、２分の１より大きいということになりますし、これは範囲外ですね。

そして、６分の３の分子にルート３を引いた数は、２分の１より小さいということになります。

さらにこれの分子の部分を観察すると、３－ルート３は

大－小でプラス

なので、コレは０より大きいということになって

ｘの範囲を満たすということがわかりました。

灘高校の数学～食塩水の濃度を求める過去問は難問だった！

これで灘高校の数学、2017年の入試問題（過去問）の食塩水の濃度を求める応用問題の解答解説は以上になります。

誘導問題の小問から、出題意図を汲み取る力を試される、東大入試を見据えた、かなりの良問でしたね☆

ご覧いただいてありがとうございました☆

どうもお疲れ様です☆