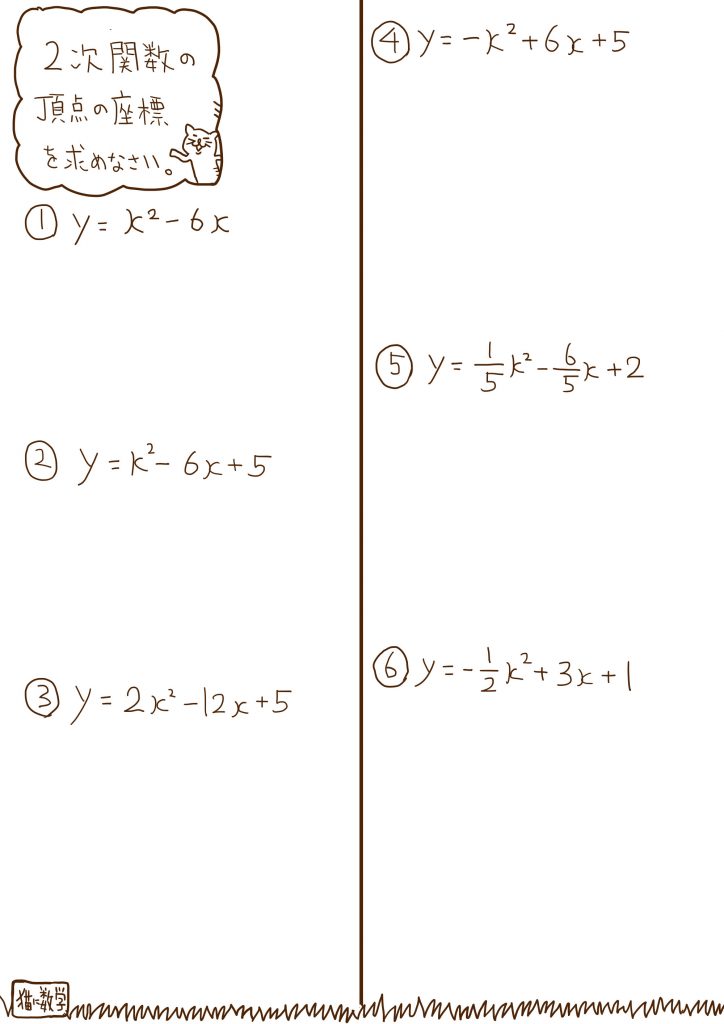平方完成の方法とコツについて無料の練習問題プリントで解説

今回は、二次関数の頂点の座標を求めるための平方完成の手順を解説します。
平方完成の方法やコツについて、練習問題の無料プリントをPDFダウンロードしていただけます。
下の画像をクリックすると練習問題をPDF形式でダウンロードできます★
この問題を使って、平方完成の手順をそえぞれ解説していきます☆
また、平方完成をしないで、頂点の座標を簡単に求める方法も別にありますので、それはまた次回、お話しようと思います。
これは、プリントと同じ問題です。

それでは、①から⑥までの練習問題を順に説明していきます。

まず、①の問題です。
上から2行目の式をご覧ください。
\(+3^2\)と
\(-3^2\)とが
書き加えられていますね。
ここの部分は合計するとゼロなので、もとの二次方程式に、結局ゼロを加えたことになり、左辺と右辺のイコール関係は依然として保たれたままですね。
3という数字はどこからチョイスしたのかというと、問題の二次方程式のなかのxの係数である-6の部分から作ります。
マイナスの符号は無視して、6という数字の半分である3を使うことになるという訳です。
なぜこのような操作が必要かというと、それは次の行でわかります。
2行目の黄色い線の部分が3行目では因数分解された形になっていますね。
このように、因数分解できる形になるよう2行目の段階で準備しておきたかったので、3の2乗という値を登場させる必要があった、ということなのです。
ピンとこないという方は、3行目にある因数分解された
\((x-3)^2\)
の部分を展開してください。
2行目の黄色い線の部分の式と同じになることが確認できると思います。
因数分解の手順ですが、公式を当てはめて因数分解してもいいですし、
たして(\(3^2\)である)9になって
かけて、-6になる数字
の組み合わせを探してもいいです。
つまり、-3と-3という数字の組み合わせを探し出して
それを使って、因数分解してもいいということです。
2行目から3行目への変形は、慣れるまで、実際に手を動かして練習してください。
慣れてくれば、-6の半分である-3を使えばいいということが、すぐにわかるようになってきます。
もっと慣れてきたら、1行目から3行目にショートカットすることもできるようになります。
それがこれですね。

1行目の-6の半分にあたる-3を、2乗のかたまりになっている(カッコ)のなかに、ご覧のように放り込みます。
それから-3の符号の部分は無視して2乗します。
3の2乗ですね。
そいつを先程の2乗のかたまりの後ろに-の符号をつけて書き加えます。
この項の符号は常に-なので気をつけてください。
たとえば、今は
\((x-3)^2\)
になっていますが
これが
\((x+3)^2\)
という形であっても
それに続く項は\(-3^2\)です。
常に「2乗したものを引く」と、覚えてもらうといいかと思います。
平方完成の手順はこのようになります。
最終的に、頂点の座標は一番下の式を見ながら解答することになります。
二次関数の頂点の座標がわかる形をしていますね。
結局この二次関数は
\(y=x^2\)
の関数のグラフを
x軸の+の方向へ3
(つまり右へ3)
ずらして
y軸の-の方向へ9
(つまり下へ9)
ずらしたものだということがわかります。
なので頂点の座標は
x=3
y=-9
ということになります。
このあたりの内容は、前回の動画である2次関数の基本的な説明で話しましたので、わからない方はそちらをご覧ください。
それでは②の問題へと移ります。

これは先程の問題の末尾に+5を書き加えたものです。
このような形になっていたとしても、+5という項は最後のほうまでいじらずに、
\((x-3)^2\)
という平方完成ができてからまとめてください。
すると一番下のような式になります。

手順を省略しない場合も、ご覧のようになります。
+5という項は3行目までは、いじらずにとっておいて、
\((x-3)^2\)
という平方完成ができてから、最後の行でまとめてください。
つづいて③の問題に移ります。
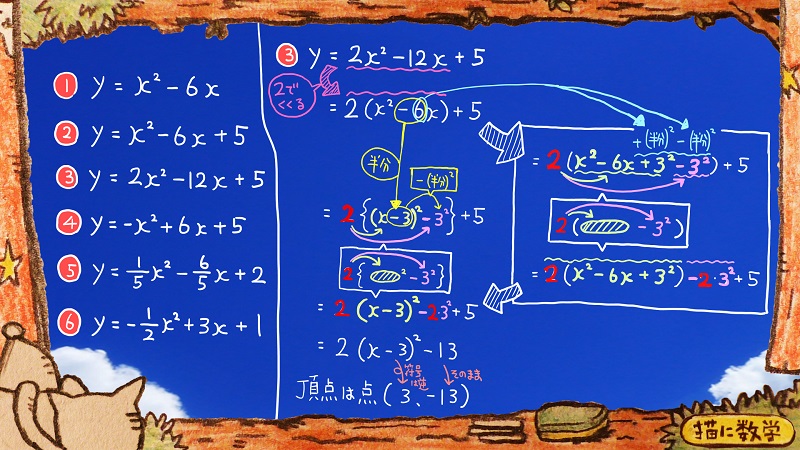
二次方程式の1行目を見てください。
xの2乗の項の係数が2になっていますよね。
さっきまでは、xの2乗の項の係数はずっと1でした。
今回のように、xの2乗の項の係数が1でない場合、先程までのやり方をいきなり使うわけにはいきません。
まず、xの2乗の項の係数である2を、くくり出す必要があります。
今回も、最後の定数項である+5は放っておいて、その手前である-12xまでの項を対象に、2でくくり出します。
すると2行目のようになりましたね。
2でくくり出された右側は、これまでやってきた
\((x^2-6x)\)のかたちになっています。
このなかだけ見れば、xの2乗の項の係数は1になっていますね。
なので、このカッコのなかの部分だけ、先程のように
変形していくことができます。
右の四角い囲みの部分を見てください。
6の半分である3、の2乗を+にしたものと-にしたものを書き加えていますね。
また、この式の緑の部分は因数分解できます。
すると
右の四角い囲みから外れて、上から3行目の式になります。
慣れてきたら、2行目からいきなり3行目の式に変形してもいい、という話もしていましたよね。
これを左側のルート、とするなら、先程の右の四角い囲みの部分は右側のルート、にあたります。
右側のルートで平方完成させる手順をまずは説明します。
四角の囲みの中にさらに小さな四角の囲みがありますが、まずは、そこで説明されていることをします。
つまり、赤く書かれた2という数字がありますが、今度はこの2を(カッコ)のなかの二つの塊に対して掛け合わせて、部分的に展開させます。
ひとつめは緑で書かれた項のかたまりに対して
ふたつめは紫で書かれた-(3の2乗)という項に対して
それぞれを2をかけていきます。
するとその下に書かれた形になります。
\(2(x^2-6x+3^2)-2・3^2+5\)
緑の部分は因数分解できますし、後ろの
\(-2・3^2+5\)
の部分はまとめることができます。
これでこの方程式は平方完成できたということになります。
つづいて左側のルートですが、3行目の式から説明をします。
これもさっきと同様に、赤色の2をかけて二重カッコを外します。
二重カッコのなかの二つの塊に対して掛けていきます。
ひとつめは緑のかたまり
\((x-3)^2\)、のかたまりですね。
ふたつめは紫で書かれた
\(-(3^2)\)という項になります。
すると、4行目のようになります。
最後は、後ろの
\(-2・3^2+5\)
の部分をまとめて完了、ということになります。
このように、xの2乗の項の係数が1じゃなかったとき、二次方程式の平方完成は、練習による慣れが必要になってきます。
二通りの手順をご覧にいれましたが、右側のルートでも左側のルートでもどちらでもやりやすいほうを採用してください。
次はこの手順を復習する問題です。
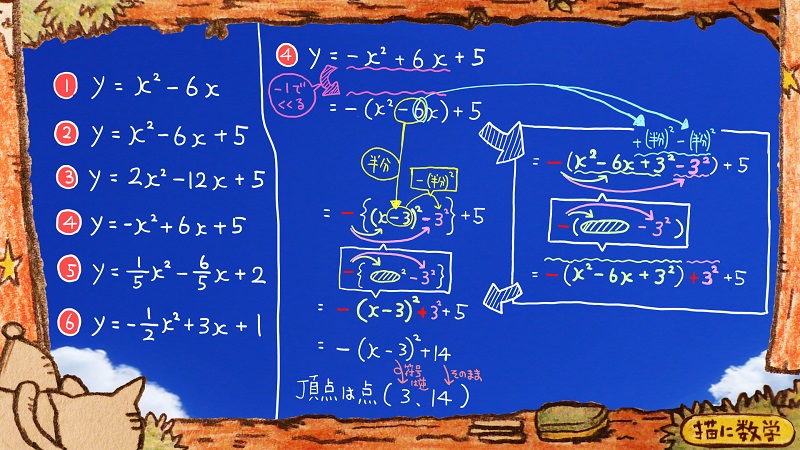
これは、xの2乗の係数が1ではなく、-1になっているケースですね。
なので、最初は-1でくくるところから変形をしていきます。
あとはすべて同様になっています。
次の⑤は、xの2乗の項の係数が分数になっている場合の問題です。
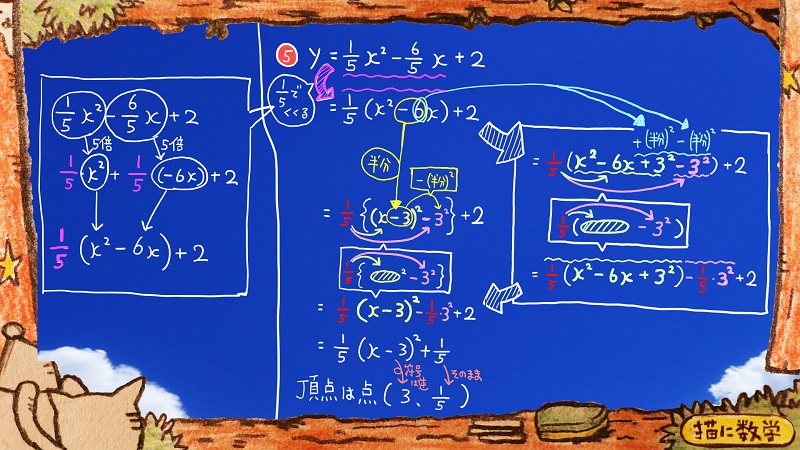
最初、5分の1でくくり出さなければいけないというところが、難しいと感じる方もいるかと思います。
なので、その方法を説明します。
左の囲みをご覧ください。
二次関数の右辺が書かれています。
これは、+2という定数項以外の項に注目してください。
5分の1をくくり出すということは、くくり出されたほうの値は5倍になっているはずだということを説明したいのですが、この書き込みでわかりますでしょうか?
「\(\frac{1}{5}x^2\)」の項は5分の1でくくり出すと、\(x^2\)になりますね。
次の「-\(\frac{6}{5}\)x」の項は5分の1でくくり出すと、5倍の-6になっていなければなりません。
なぜなら、5分の1でくくり出された左下の式を展開すれば、くくり出す前の式に戻るはずです。
なので、
5分の1をかけてもとに戻るためには、かけられる値はもとの5倍でないと、ぴったりもとにもどらない。
ということになります。
簡単に言うと、くくり出す値の逆数をかけてやれば、展開したときにもとに戻る、ということになります。
逆数というのは、分母と分子がひっくり返った値のことです。
5分の1の逆数は、1分の5、つまり5ということになります。
5倍する、という書き込みがあるのは、5分の1の逆数からきています。
この問題で新たに説明すべきことはこれくらいです。
それ以外はこれまでと同じ手順で導くことができます。
では最後の問題に進みます。
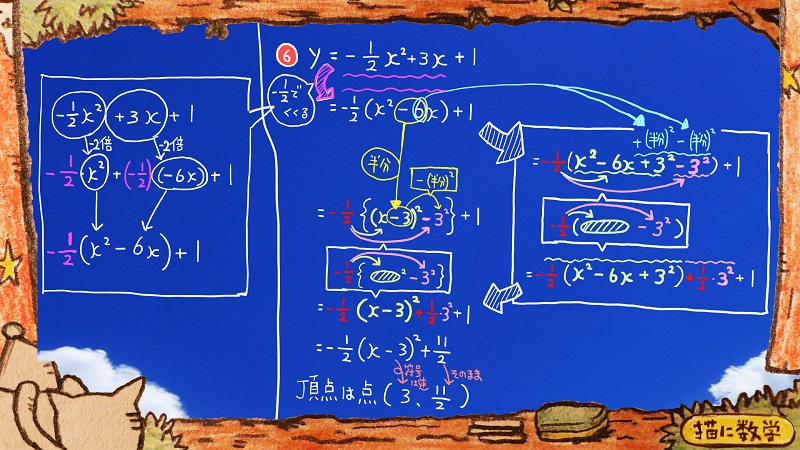
これも最初の分数でくくり出すところが前の問題と同じです。
-2分の1の逆数は-2なので、くくり出された項の値は、-2倍になっています。
これもまた、そのあとの解答は同じ手順になります。

いかがでしたでしょうか?
これは、平方完成の過程を文字で説明したものです。
これを使えば、今回やったような平方完成の手順を踏まなくても、頂点の座標をもとめることが可能です。
また、これ以外にも、因数分解によってグラフとx軸との交点をもとめて、そこから頂点の座標を求めてゆく方法もあります。
高卒認定試験の新数学で、この内容が必要な方は、平方完成の手順をマスターするよりも、こっちの方法が有効ですから是非ともご覧ください。
それらはまた次回にお話ししますので、今回はここまでにさせていただきます。
平方完成の方法とコツの解説は以上になります。
これで平方完成の方法と、コツについての説明は終了します。
あとは、頂点の座標を求めて、二次関数のかたちをグラフで書くことができれば、数Ⅰの問題の最初の基礎の部分ができた、ということになります。
無料でダウンロードできるプリントを今回使用しましたが
慣れるまでは実際に練習問題を手を動かして解いていただければと思います。
お疲れさまでした☆