数Ⅰで学習する二次関数と二次不等式の解き方の違いについて

今回は、高校数学の数Ⅰで習う二次関数と二次不等式のエッセンスをざっと５分ほどで(非常に短時間で)解説しようと思います。

この分野を学習する前に、「これからこんなこと習うんや」という大枠をつかみ取ってもらうための解説です。

特にこの分野の話がややこしかったという方は、これを見てからだと、ほかの説明に対する理解度も変わってきます。

また、具体的な問題を解くことになったとしても、自分が今、どういった問題を解いているのか把握しやすくなるでしょう。

なので、学校の授業がわからなかったという方も一度ご覧いただければと思います。

二次関数とは

まず二次関数についてお話していきます。

中学３年生の数学で、習っていた内容がこの形ですね。

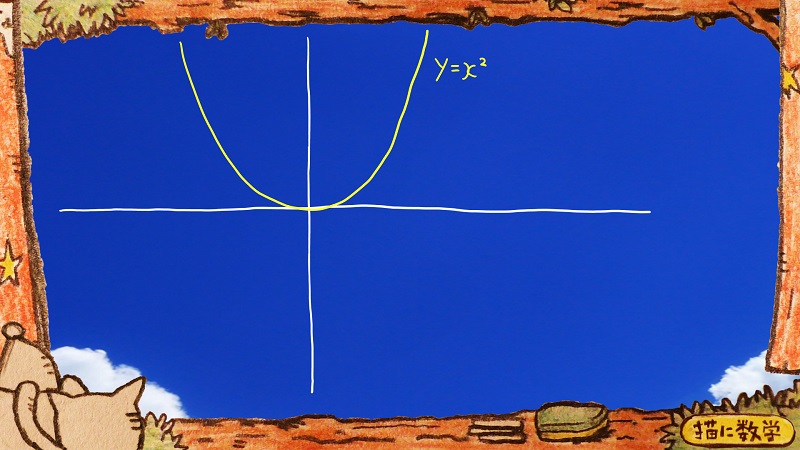
これはｘの二乗という関数をグラフで表したものです。

ちなみに書くのを忘れていたのですが、今回登場するグラフは横軸がｘで縦軸がｙとなっています。

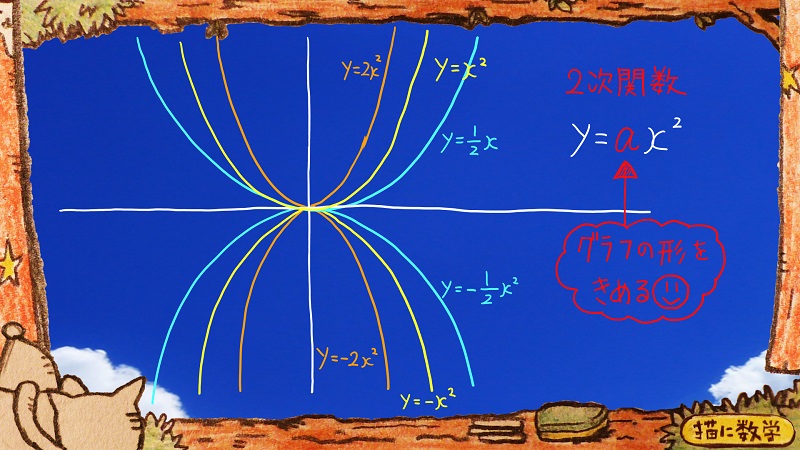
さて、この二次関数のグラフですが、ｘの二乗にかかっている係数aというものが書かれていますね。

このaは、１であった場合、表記を省略されています。

画面には、係数が２の場合や１の場合、２分の１の場合など書かれていますね。

また係数がマイナスになるとグラフの形がひっくりかえったようになります。

つまり、aによってグラフの形が決定される、ということがわかるかと思います。

さて、中学数学の復習ができたところで、ここからいよいよ高校数学の内容に進みましょう。

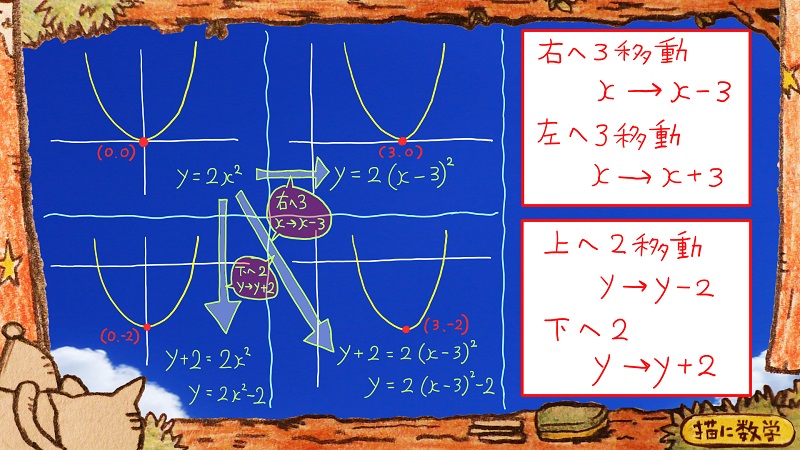
グラフが４つありますが、まず、左上のグラフをご覧ください。

これは、原点のところに二次関数のグラフの頂点があります。

ここのｙ＝２ｘの二乗という表記は見慣れたものですね。

このグラフを、例えば右へ３並行移動させたいとします。

ｘ軸の方向で＋３移動させたい、ということですね。

この場合

もとの二次関数の式に対して、

ｘをｘ－３に書き換えると、その移動後の関数を表現することができます。

すると右上のグラフになって、

その二次関数は

\(ｙ＝２(ｘ－３)^2\)、という式になりましたね。

ちなみに今のは右へ３移動させる場合でしたが、左へ３移動させたい場合は、

ｘをｘ＋３に書き換えます。

つまり、

ｘ軸の方向で＋のほうへ移動させたい場合は

ｘをｘ－何とか、という表現に変えて

ｘ軸の方向で－のほうへ移動させたい場合は

ｘをｘ＋何とか、という表現に変えるというわけです。

これが横移動の手順になります。

続いて縦移動ですが

これも同じ要領です。

ｙ軸の方向で＋２移動させたい場合

つまり、上に２移動させたい場合は、

ｙをｙ－２、という表現に変えます。

逆にｙ軸の方向で－２移動させたい場合

つまり、下に２移動させたい場合は

ｙをｙ＋２、という表現に書き変えます。

ちょうど左下のグラフが、もとのグラフから、下に２移動させたグラフになっていますね。

そして右下のグラフは、もとのｙ＝２ｘの二乗というもとのグラフから、右に３移動させ、下に２移動させていますね。

その場合は、

ｘをｘ－３に置き換え

ｙをｙ＋２に置き換えています。

＋２の部分を見やすいように方程式の右辺のほうに移項したかたちも書いていますね。

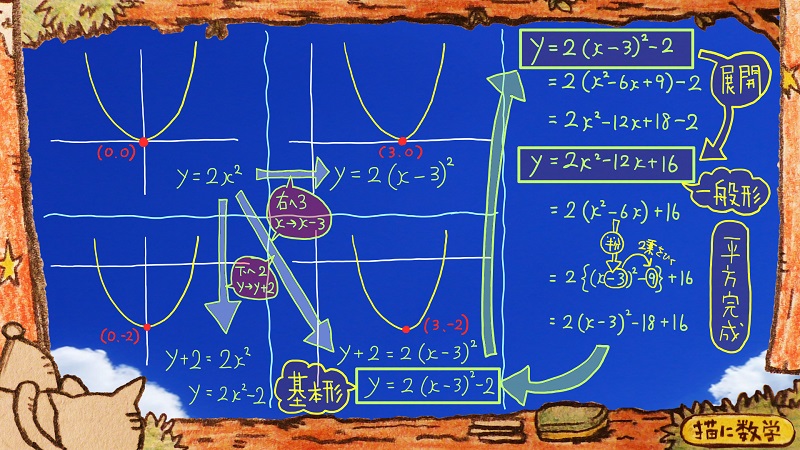
これは基本形と言って、この形で書いてあると、グラフの頂点の座標がわかるようになっています。

右辺の一番右にある－２という項は、そのまま頂点のｙ座標である－２になっていますね。

また、ｘ－３のなかの－３は、符号を逆にすれば、頂点のｘ座標である３という数字に一致します。

このように基本形で二次関数が表現されている場合は、一番しっぽの部分にある項はそのまま頂点のｙ座標としてとらえて、ｘの後ろについている数字は符号を逆にすると、それが頂点のｘ座標にあたる数字だということですね。

また、左上のグラフを見てみると、グラフのかたちをきめている数字はｘの２乗にかかっている２という係数ですが、その係数は、たとえグラフをどのように平行移動させたとしても、２という表示は崩れていないですね。

右下の基本形にも、ちゃんと２という数字は残っています。

たとえばこいつがもし－２だったら頂点はそのままで、グラフの形が上下に反転するということです。

二次関数と二次方程式との関係って？

それでは、右半分に書いているところの説明に移ります。

二次関数の基本形が一番上に書いてあります。

これを展開すると、一般形と呼ばれる形になります。

これは、ｘについての降べきの順にならぶかたちになっていて、とても見やすい形をしています。

この一般形も、さっきの基本形も、同じ二次関数を表現していて、グラフにすると同じものになります。

ただ、この基本形のままでは、グラフの頂点の座標がわかりませんね。

なので、これをさっきの基本形になおす手順も必要になってきます。

基本形にはｘ－３の２乗というように２乗のかたまりで出来ていますね。

このように２乗の形をつくりだすことを「平方完成」と言います。

詳しい手順と練習問題はまたこちらの授業↓にてご紹介します。

平方完成の方法の授業

また、平方完成しないで頂点を求める方法もありますので、これもまた次回お話できればと思います。

とりあえずここでは、二次関数の表現にはこういったものがある、ということだけおさえておいてください。

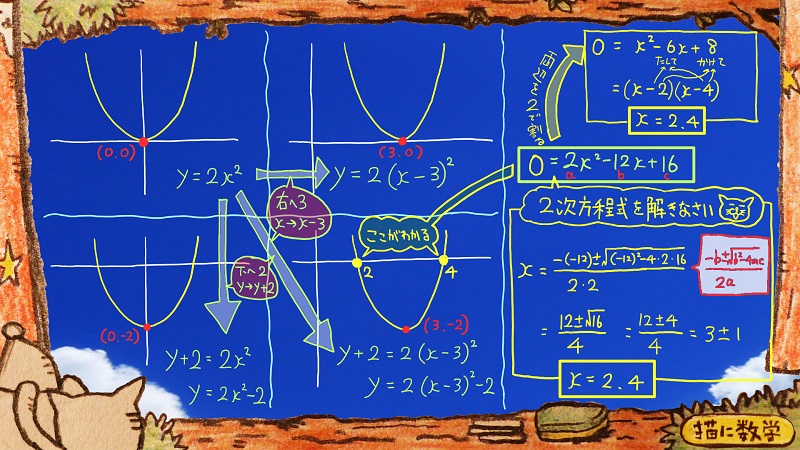
続いてグラフとｘ軸との交点を求める方法についてお話します。

中学３年生の数学で、このような「二次方程式を解く問題」を練習していたと思います。

これは、左辺が０になっていますが、この部分は先程ｙが書かれていましたね。

ｙ座標はグラフの縦軸の情報にあたるので、この場合、

このグラフの高さにあたるｙの数値が０のとき、つまりグラフの高さが０になっているとき、ｘ座標の数値は何ですか？

と聞いているようなもの、だと思ってください。

ｙ座標が０になるためには、この式のなかのｘがどのような数字であればいいですか？

と聞いているようなものです。

つまりこの二次方程式を解くという工程は、

グラフとｘ軸とが交わるポイントのｘ座標を求める工程

とも、とらえることができます。

では実際に解いてみます。

この場合は、因数分解して解く方法と、解の公式を使って解く方法があります。

因数分解する方法ですが、

まず、方程式の右辺の項の定数の部分を見ると、すべて２の倍数になっていますよね。

２も、－１２も＋１６もすべて２の倍数ですよね。

なので、両辺をまず２で割ります。

すると、すっきりした形になりましたので、

かけて＋８になる数字で、なおかつ

たして－６になる数字の組み合わせを探します。

－２と－４がそれに当たりますので

ご覧のように、その数字で因数分解ができるということですね。

解はｘ＝２または４になりました。

この２または４というのはグラフで見ると、黄色い点の部分のｘ座標の情報になります。

さっきもお話しましたが、この二次方程式を解くことはつまり

グラフの高さにあたるｙが０になっているとき、つまり、グラフの高さが０の時、ｘの値は何であればいいですか？

という質問を解いたようなものです。

なので、ｘが２または４のとき、高さにあたるｙはちょうど０になっていることになります。

また、解の公式を使ってｘを求める方法もあります。

解の公式にあてはめて解くと、先程と同じｘの値がふたつ出てきましたね。

ただ、今回はグラフの頂点がちょうどｘ軸の下側にあったので、ｘ軸との交点は二つ存在していました。

けれども、もしも頂点がｘ軸よりも上のほうに浮いている状態だったらどうでしょうか？

ｘ軸との交点は存在しないことになりますね？

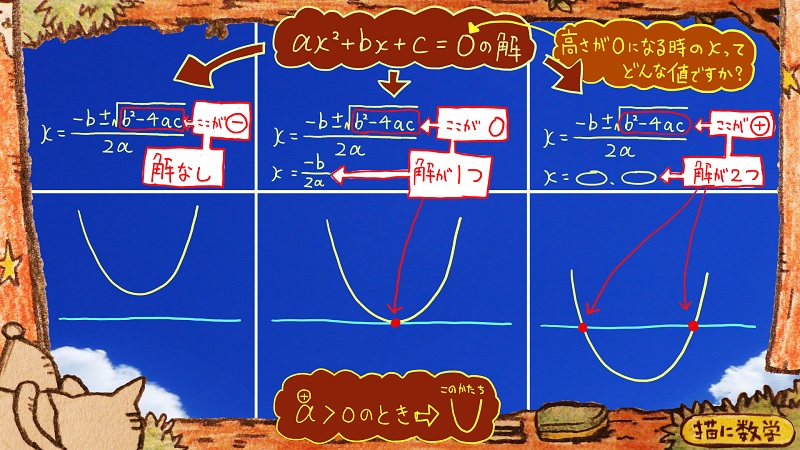
この図の左側にあるグラフがまさにそのような状況ですね。

二次方程式が一番上に表示されていますが、もしもこれを解こうとして、解の公式を使った場合、グラフの状況に応じて、３パターンの結果が考えられます。

先程、解が二つ出たのが、一番右の状況ですね。

解の公式を使ったとき、ルートの中に当たる計算部分の符号が＋になっていたと思います。

なので、±√という形が保たれて、最終的に解が二つ表れたということでしたね。

つまり、√の中の「\(b^2－４ac\)」の計算結果の符号が＋だった場合、解は二つ表れるということがわかります。

それでは、√の中の「\(b^2－４ac\)」の部分がちょうど０だった場合、どうなるでしょうか？

それが真ん中のグラフのパターンです。

√のなかが０になることで、ちょうど±√という固まりが消えてくれることになります。

なので、解は１個だけ導き出されるということになります。

これってつまり、真ん中のグラフのように、ｙ座標、つまり高さが０になるときのポイントはちょうど１か所しかないという状況になっていますね。

そしてルートの中の符号が－になっている場合

√の中が－になるというのは、これまで習ってきた限りでは、ありえない状況ですね？

なので、解なし、という結果になります。

これはつまり、ｘ軸とグラフとの交点が存在しないことを示していますので、左のグラフに見られるような状況になっています。

どうでしょうか？

ざっとお話しましたが、このグラフの３パターンはｘの２乗の係数にあたるaが＋のときですね。

いま上の方程式の左辺は一般形の形をしていますが、これを、頂点の座標がわかるような基本形に変形した場合、aは二次関数の形を表現している数値のポジションにちゃんとあるということがわかります。

これは先程表示していた画面です。

一般形の式の部分に「\(２ｘ^2\)」がありますね。

この「２」という数字ですが、これって基本形に直したとしても、この数字は崩れないまま残っていますよね。

基本形の式からこのグラフは、もともとｙ＝２ｘの二乗という関数を平行移動させて作られたものとして読み取ることができますね。

先程の一般形にあった「\(ax^2\)」のaは、そのままグラフの形を表現している数値だ、ということが理解していただけたでしょうか？

さっきの図にもどります。

この３パターンの状況は、グラフの形を決定するaの符号が＋であった時のものになります。

もしaの符号が－であったら、このようになります。

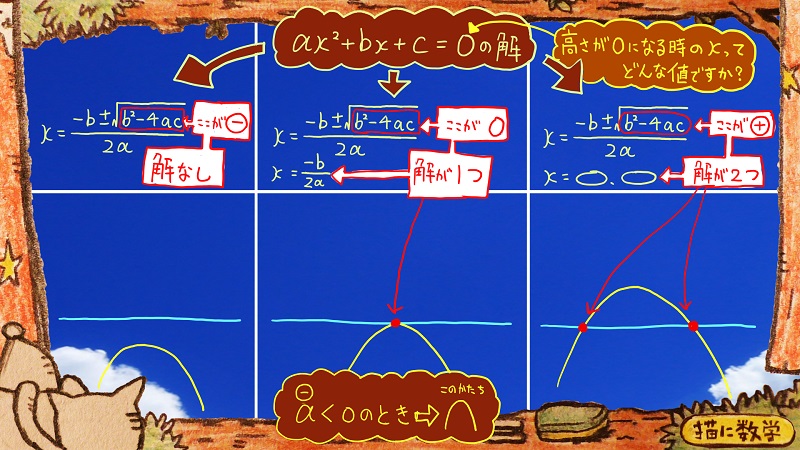
グラフの形はさっきとは上下に反対の形になりますね。

その形のまま、解が２つのとき、解が１個のとき、解がないとき、の状況をグラフにすると、ご覧の３パターンになります。

中学数学で、二次方程式を解いていたと思います。

それってつまり、この表で言う、解が２個のときか、あるいは解が１個の時の、ｘの値を計算して求めていたということですね。

では、この流れを引き継いでそのまま二次不等式の話をします。

一番上の式を見ると、先ほどの二次方程式のイコールの部分に「大なり」という符号を書き加えました。

これは、まず左辺の塊を見てください。

「\(ax^2＋bx＋c\)」とあります。

この中のxの部分は「x座標を表す数値」に相当するものですが、

「\(ax^2＋bx＋c\)」という塊そのものはy座標の数値を表している、

と思ってもらうと、不等式の意味もわかりやすいかと思います。

実際グラフを書くときは、

「\(ax^2＋bx＋c\)」＝「ｙ」

というようにｙを定義して

ｙを縦軸

ｘを横軸

としてグラフを書きます。

なので、この二次不等式の意味は

グラフを書いたときに高さに相当するｙの部分

つまり

「\(ax^2＋bx＋c\)」の部分が

０以上のときになる場合、

そのときｘはどの範囲にあるとそうなるんですか？

というｘの範囲について聞いている

と思ってもらうといいです。

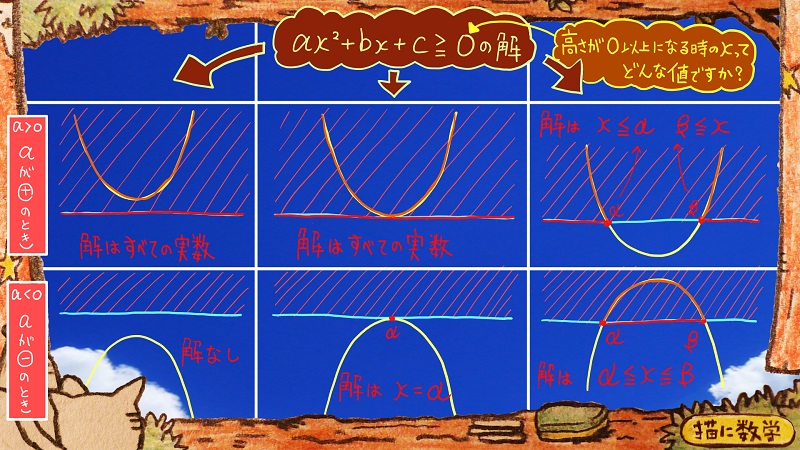
aが＋のときは上の３パターン

aが－のときは下の３パターンに

それぞれ考えられるグラフの状況があります。

もしも、この二次不等式の不等号がないものとして計算した場合、つまり＝０だとして二次方程式の解を求めた場合、先ほどがそうであったように、ｘ軸との交点にあたる部分のｘ座標が現れますよね。

交点が２個ある場合は右側のパターンですし、交点が１個の場合は真ん中のパターン、交点がない場合は左側のパターンですね。

さらにaの符号がどうであるかによって、この６つのグラフの状況のなかのどれか、ということがわかります。

この状況がわかるとあとはそのグラフを見ながら、解答していくことができます。

それぞれ見ていきましょう。

右上のグラフから説明します。

これは交点が二つあった場合ですね。

交点のｘ座標の数値をα（アルファ）、β（ベータ）とします。

このグラフにおいて、高さが０以上になっている時のｘの範囲を見ると、α以下の範囲、とβ以上の範囲、ということがわかりますでしょうか。

ｘ座標においてαからβの間の範囲は、高さがマイナスのところにグラフの線がありますよね。

なのでその範囲以外の部分が答えの範囲になりますよね。

よって

この場合の解は

ｘ≦αまたはβ≦ｘ

となります。

つづいてその下のグラフをご覧ください。

こんどはグラフの形がさっきと比べて上下逆さまになっています。

αとβをふくみつつ、その間の部分だけグラフの高さがプラスの領域に書かれています。

それ以外のｘの範囲を見ると、その時グラフの線は高さがマイナスの領域にありますね。

というわけでこの場合の解は

α≦ｘ≦β

ということになります。

次はまんなかの上を見てみましょう。

ｘがどのときも、このグラフの高さは０以上になってますよね。

なのでこの場合の解は

すべての実数

ということになります。

つづいてその下です。

グラフの線は、ほとんどすべて高さがマイナスのゾーンにありますが、唯一ｘ軸との交点においてだけ、高さが０になっています。

この時のｘ座標の数値をαとするなら、解は

ｘ＝α

ということになります。

次は左上のグラフです。

これはグラフがｘ軸よりも浮いている状況なので、ｘ座標がどんなときであっても高さは常に０以上ということになりますね。

なので解は

すべての実数

ということになります。

さあ最後はその下です。

これはグラフはｘ軸にふれることもなく下に沈んでいる状況ですので、高さが０以上になることはありません。

なので、この場合

解はなし

ということになります。

どうでしょうか？

ちょっと理解いただけましたでしょうか？

ちなみにこれは不等号に＝があった場合の状況でしたが、イコールのない二次不等式だと、このようになります。

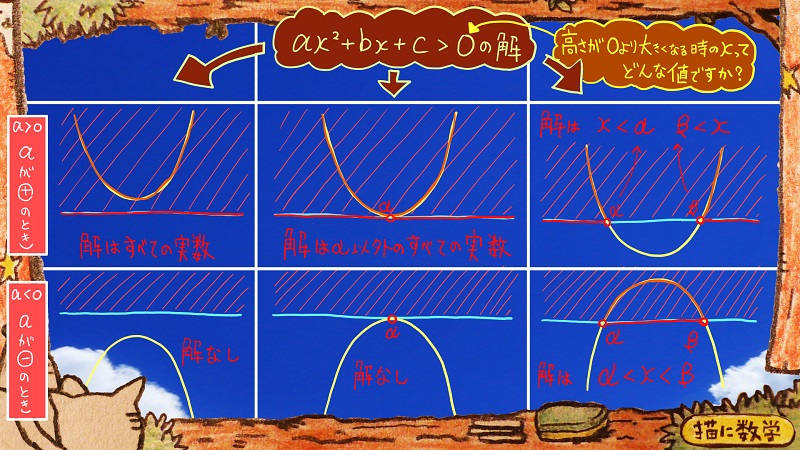
さっきは高さが０の時もアリだったのですが

これだと高さが０のときはナシになっていますね。

つまり

グラフの高さが０より大きくなるときのｘの範囲を求めよ。

という内容に変わっています。

なので、左側の２つのパターンの解は、それぞれ先程と変わらないのですが、まんなか２つと右側２つのパターンは、答え方がかわってきます。

右側ふたつのパターンですが、まず、高さが０になるときはナシになったので、解答している部分の不等号から＝が消えていますね。

これってつまりｘ座標の数値がαやβのときはちょうどグラフの高さが０になるときだから、その場合だけ除外した、ということです。

さっきの場合は、グラフの高さが０になるときであるｘ座標のαとβは、解の範囲に入れてもよかったのでイコールをつけていたということですね。

真ん中の上のグラフを見てみましょう。

さっきの場合は、ここの解は『すべての実数』となっていたと思います。

けれども今回は、ｘ座標がαのときだけ、グラフの高さが０になってしまいます。

なので、ｘ座標がαの時以外は、グラフの高さは０より大きくなってくれるので、解は

α以外のすべての実数

ということになります。

では、その下を見てみましょう。

さっきはここの解は

ｘ＝αになっていました。

ｘ座標がαのときだけグラフの高さが０になっていたからです。

ただ、今回は、グラフの高さが０のときはナシになっているので、ｘ＝αのときであっても、それを解とすることができなくなりました。

なので、この場合

解なし

ということになります。

どうでしょうか？

だいたいこれで二次不等式のつかみの部分は話せたと思います。

最後に不等号がひっくり帰ったパターンをご覧にいれて終わりにしたいと思います。

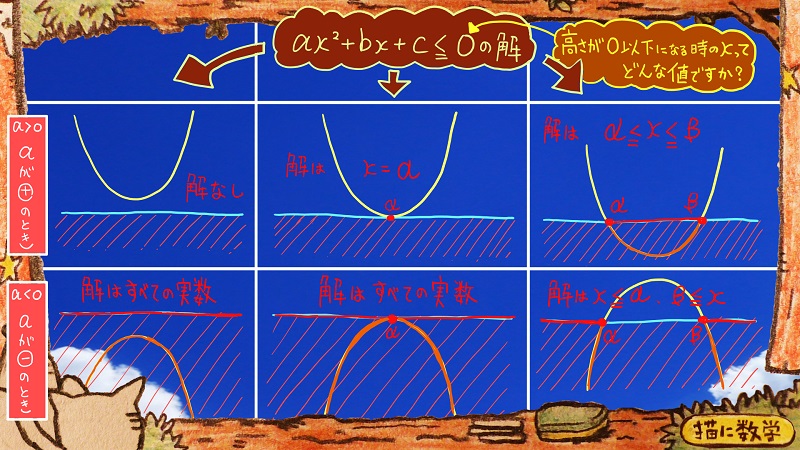
これは不等号が≦になっている時です。

グラフを見た時にグラフの高さが０以下になっている時のｘの範囲は何ですか？

という質問ですね。

さっきご説明した考え方で一つひとつ見ていくと

理解できるかと思います。

はっきり言って僕はこんなパターンは覚えていません。

その都度、グラフを書いて状況を確かめれば済む話です。

ここで理解してほしいことは、二次不等式の読み取り方ですね。

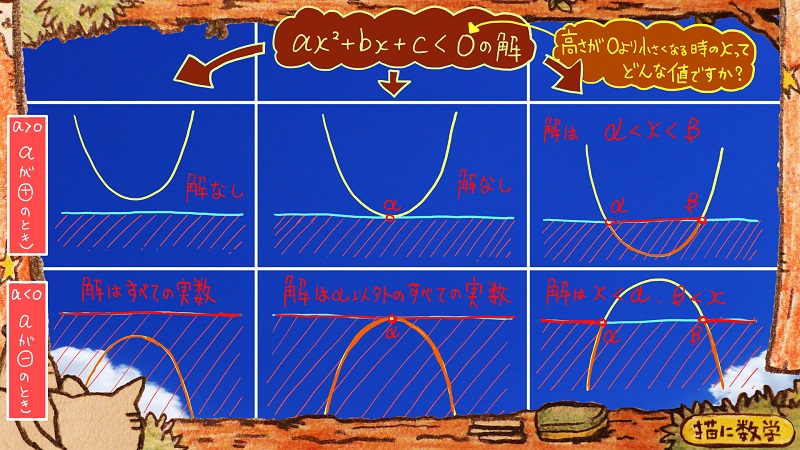
これだとこの二次不等式は、

「ｙ」＝「\(ax^2＋bx＋c\)」

というグラフを書いたときに

そのグラフの高さが、０より小さくなるときのｘの範囲って何なんだろ？

というように考えられればいいワケです。

あとはグラフを書いて、それを見ながら考えればいいですよね。

以上、今回は高校数学の数Ⅰで学習する、二次関数と二次不等式のおおまかな内容についてざっと解説しました。

このあたりの理解を深めたい方は次の講座もご覧ください☆