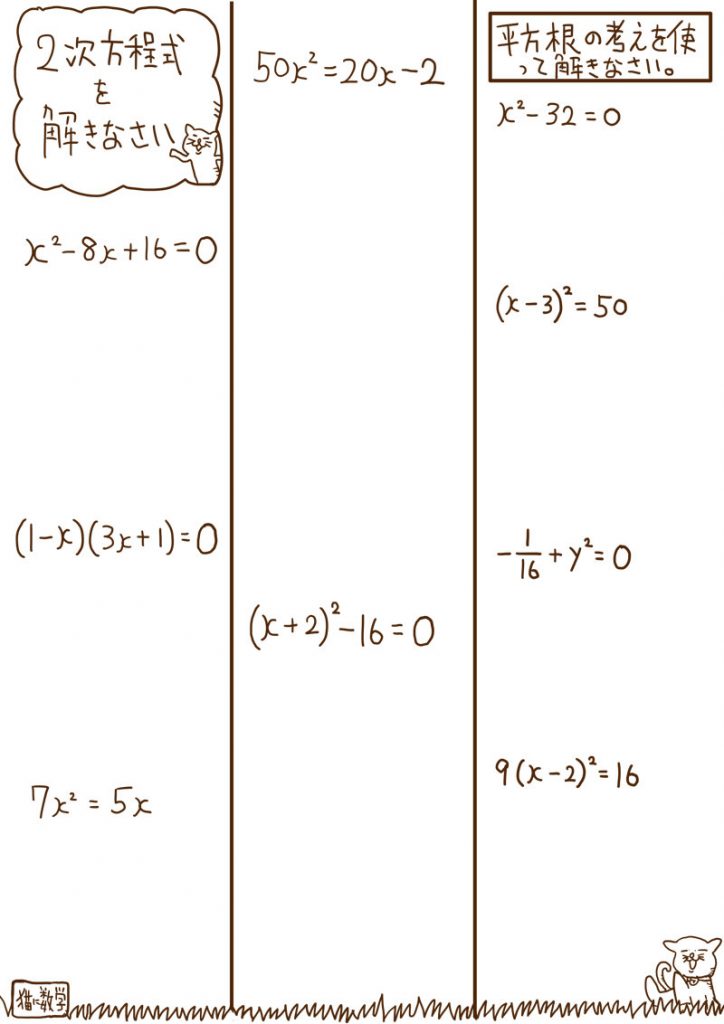
中3数学「二次方程式の解き方と因数分解」解の公式の覚え方と簡単な計算問題

今回は中学3年の数学で学習する、因数分解や解の公式を利用した、二次方程式の解き方についてお話しようと思います。
これを見れば、基本パターンはすべて網羅できるようになっています。
一通りの手順を解説しましたら、後半からこの練習プリントの問題を解説していきます。
これはPDF形式の無料でダウンロードいただけるプリントですので、必要な方は、この下のプリント画像をクリックしてください☆ダウンロードできる表示に切り替わります。
また、この練習問題は、公立高校入試の対策や中学3年生の定期テスト対策にも利用してください。
それではここからは、この問題の解答・解説授業もご覧いただける授業動画をご視聴ください☆
以下はこの内容の板書になります。
それでは、さっそく始めていきましょう。

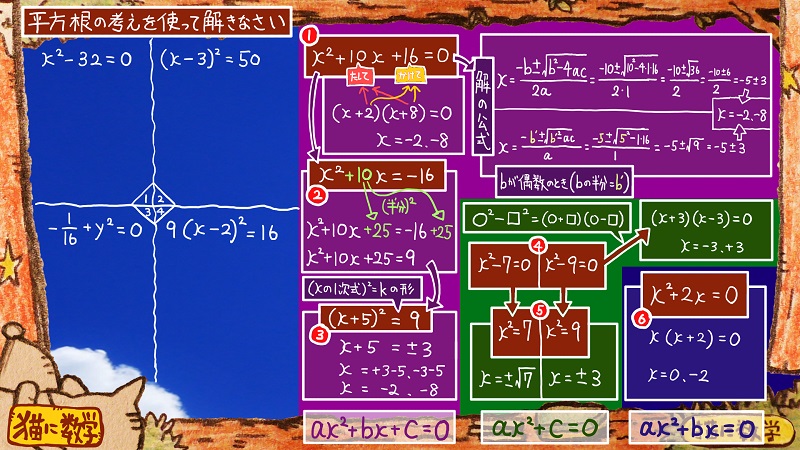
まず、右側の画面は紫色のゾーンと緑色のゾーンと青色のゾーンの三種類にわけてまとめています。
それぞれ、二次方程式の形のパターンによって色分けしているのですが、とりあえず一番ちいさな青色のゾーンから説明していきます。
これは、二次方程式の形のなかでも数字だけの項がないパターンですね。
xも、xの2乗も掛かっていない数字だけの項がここにはないですよね。
左側の例題には
xの2乗+2x=0
とあります。
xの2乗にも、2xにもどちらもxが1個共通して掛かっていますね。
これを共通因数といいます。
この共通因数である1個のxを先頭にくくり出します。
どうでしょうか?
xと(xたす2)が掛け算の形でつながった形になったと思います。
このように、すべて掛け算の形につながった形に変形することを因数分解するといいます。
たとえば6は3×2という掛け算の形に分解できますね。
2と3は、6という数字をつくる原因になっている数ですよね。
因数に分解するというのは、こういうことです。
とくにこの場合は、2も3も素数なので、素因数に分解する「素因数分解」という工程になります。

さて、さきほど因数分解した方程式の左辺を見てみましょう。
xと(x+2)の二つの因数がありますが
黄色のxの部分が0だった場合は、その右側の(x+2)がどんな数であったとしても、「0かける何か」のかたちになりますので、イコールゼロになって、この場合、方程式は成り立ちますね。
なので、x=0は解のひとつになります。

また、(x+2)の部分が0のとき、黄色のxがどんな数であっても、掛け合わせるとイコールゼロになって、方程式が成り立ちますね。
なので、x+2が0のとき、xはなんだろうか?
という計算をすることになります。
x+2=0という方程式を解けば、その時のxが-2だということが明らかになりますよね?
というわけでx=-2というのも、解のひとつということがわかりました。
さっきの解がx=0でしたから、それも含めて解が二つ求められました。
これが青色のゾーンのパターンですね。

次に緑色のゾーンのパターンをお話します。
上のほうに「bがない」という表記がありますが、「bxがない」という意味に解釈してもらえればと思います。
今表示しているのは表のなかの⑤のパターンですね。
この問題の方程式の意味はこういうとこです。
「ある数xを2乗すると9になりますよ。さて、xはなんでしょうか?」
こういうことですね。
2乗して9になるのは+3と-3ですね。
なので、この二次方程式の解は+3と-3ということになります。
また、この二次方程式はこのように変形した形で登場することもあります。

この形のほうが「bxの項がないパターンだ」ということがよくわかりますね。
右辺をイコールゼロの形に変形してから「さてどのパターンだ?」と考えると、どの色のゾーンの問題か?ということを間違うことがないです。
この問題ですが、左辺が2乗引く2乗のかたちになっていることがわかりますでしょうか?
xの2乗はすでに2乗という表現になっていますし、9だって3の2乗ですよね。
2乗引く2乗の形になってるばあい、「公式」と書いてあるように、因数分解の公式を当てはめることができます。
ちなみにこの因数分解の公式を逆に使うと、展開の公式としても使うことができます。
ともかくこの問題の左辺は
(x+3)かける(x-3)という形に変形することができました。
ここからは⑥の問題の時と同じように考えます。
(x+3)が0のときも方程式が成り立ちますし
(x-3)が0のときも方程式が成り立ちます。
なので、
x+3=0を解いてx=-3
x-3=0を解いてx=+3
ということになります。

ちょっとここでもういちど⑤のパターンの問題を見てもらいましょう。
さっきとは右辺の数字が変わっていますね。
これも先程と同様、
「2乗して7になる数字は何になるか?」
ということを考えます。
解はx=ルート7とx=-ルート7になります。
このルートというのは平方根を求めるときに登場する記号です。
今、2乗して7になる数は?ということを考えていたわけですが。
この2乗して7になる数を求めることを「7の平方根を求める」というように表現します。
平方という言葉は、平方メートルという単位で聞いたことがあるかと思います。
あの記号ってメートルに2乗のマークがついていますよね。
平方には2乗という意味があるのですね。
たしかに正方形だったらその1辺の長さを2乗すると面積が求められますよね。
例えば
2乗して面積が7になるような正方形の1辺の長さを求めよ。
と言われれば、一辺の長さはルート7になるわけですが
これってつまり
・平方して(2乗して)7になるための、根っこの部分の数字ルート7を求めた
という言い方をすれば平方根の意味もわかりやすいかと思います。
ただ、これは長さを求める話なので、計算上はマイナスルート7も7の平方根のうちのひとつになりますよね。
さて、それではいよいよ、一番広い、紫のゾーンにある解法のパターンについて解説していきます。

この二次方程式のパターンは、bxもcも登場しているパターンです。
まずは③の問題を見てみましょう。
これは、
左辺が、なにかの2乗
右辺が、xのついていない数字
になっていますね。
これってさっき平方根のお話をした⑤のパターンと同じですね。
なので、同じ解き方ができます。
赤い四角で囲まれた部分を見てください。
(x+5)の部分をひとつの数字だとみなすと、この部分は結局+3または-3だということがわかりますね。
つまり
(x+5)の部分が+3のときのxを求めて
(x+5)の部分が-3のときのxを求めればいい
ということがわかります。
(x+5)の部分が+3のときは
(x+5)=3になりますね。
これを解くとx=-2になります。
(x+5)の部分が-3のときは
(x+5)=-3になりますね。
これを解くとx=-8になります。
結局xは-2と-8であるということがわかりました。
特に中学生に覚えておいて欲しいのですが、
もし問題文に
「平方根の考えを使って解きなさい」
などと書いてあった場合は、この解き方でないといけません。
あとで説明しますように、展開してから全体を因数分解したり、解の公式を使って解くという別の方法はしないでください。
次のその展開して解く方法について説明します。

まず、さっきの問題である③のかたちを右表の①のかたちにしてから因数分解で解く、という手順をお話します。
これはまず、左辺に対して展開の公式を使うのですが、公式を覚えていなくても
(x+5)かける(x+5)を分配法則にしたがって展開していけば、同じ結果になります。
展開した左辺に、さらに右辺にある9を左辺に移項すれば、①の二次方程式になります。
それを因数分解する方法ですが
まず、xのついていない16を見ます。
かけて16になる二つの数字は何かな?と考えます。
1と16とか
2と8とか
4と4とか
-1と-16とか
いろいろ出てくると思います。
次に、10xの項を見ます。
xの係数の10に注目します。
さっきあげたペアの数字のなかから
今度は足して10になる数字のペアを探します。
この場合、2と8がそれにあたりますね。
それを下の式のように因数分解した形に放り込んで完成させます。
(x+2)(x+8)=0が完成しました。
あとはもうお分かりですね。
(x+2)の部分が0のとき、方程式は成り立つので
その時のxを求めるとx=-2になります。
(x+8)の部分が0のときも、方程式は成り立つので
その時のxを求めるとx=-8になります。
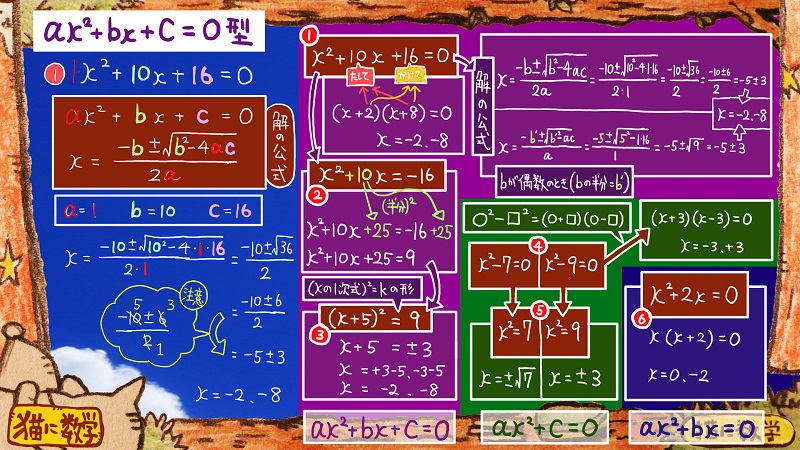
さあ次は、二次方程式の解の公式を使った解法を覚えてもらいます。
「解の公式」と書かれた茶色い四角い囲みが、左側にありますのでご覧下さい。
二次方程式の右辺を0にしたときに、それぞれ各項の係数がありますね。
この場合、公式には
xの2乗の項の係数はaと書いてありますね。
例題では
xの2乗の項の係数は省略されていますが1がそれにあたります。
なので公式のaに該当するのは1になります。
また、公式には
xの項の係数にはbが書いてありますね。
例題では
xの項の係数は10とあります。
なので公式のbに該当するのは10ということになります。
また、公式のCに該当するのは
数字だけの部分なので16ということになります。
a=1
b=10
c=16
ということがわかったので、それを茶色の囲みにあるごちゃごちゃした解の公式に当てはめて解きます。
二次方程式の解の公式の覚え方ですが、これは30回ぐらい声に出してくりかえせばだいぶ覚えられます。
結構長いので
にーえーぶんのまいなすびー
の部分と
びーにじょうまいなすよんえーしー
をそれぞれ別々に何度も繰り返して暗記してから、全体を空で言えるようになることをオススメします。
というのも、高校数学で2つのこの部分がそれぞれ活躍することになるので
どっちにせよ、聞いたことがある状態にしておくとあとで便利です。
このパターンだけもはや計算問題ですが、計算ミスだけ気をつけてください。
計算の途中に「注意」と黄色で書かれているところがありますがミスをしやすいポイントです。
-10と±6は掛け算でつながっておらず、別々の項になっています。
それを分母の2で割る場合は、まとめて割らないといけません。
-10は-5になり、±6は±3になるということですね。
よくわからない方が多い場合は、この内容だけ改めて説明しようと思いますが、ここではこれぐらいの説明にしておいて先に進みます。
解は結局、x=-2と-8になりましたね。
次は裏技というほどでもありませんが、このややこしい解の公式の計算をちょっとだけ簡単にできる方法をご紹介します。

ちなみにこれはちょっとオマケの内容になります。
今の問題ではxの係数が10になっていましたね。
この10という数字は偶数になっています。
このようにxの係数が偶数の場合に使える公式があるのでそれを紹介しておきます。
bの半分をbダッシュとします。
すると解を求めるときの式が、少し簡単になっているのがわかりますでしょうか。
さっき分母が2aだったのが、aになっていますよね。
ルートのなかの計算も、ちょっと簡単になっています。
b2乗-4ac
だったのが
bダッシュ2乗-ac
とちょっとだけ簡単になりましたね。
数字を代入したあとの計算過程もさっきと比べて結構すっきりしています。
ただ、さっき紹介した解の公式がしっかり定着できた方のみ、この方法を取り入れたい方は取り入れてください。
そして、もしも定期テストなんかで「2次方程式を解の公式を使って解きなさい」と指示があった場合は
、教科書に載っているさっきの方法で解いたほうが無難です。
ただ授業中にこの方法を習ったりしていたらおそらく使ってもいいかもしれませんが、このあたりは状況に応じて使い分けてください。
まあ、答えだけを解答させる場合は、役に立つこともあるでしょう。
ただ、くれぐれも一般的な解の公式が使えるようになってから、取り入れるかどうかを考えてください。
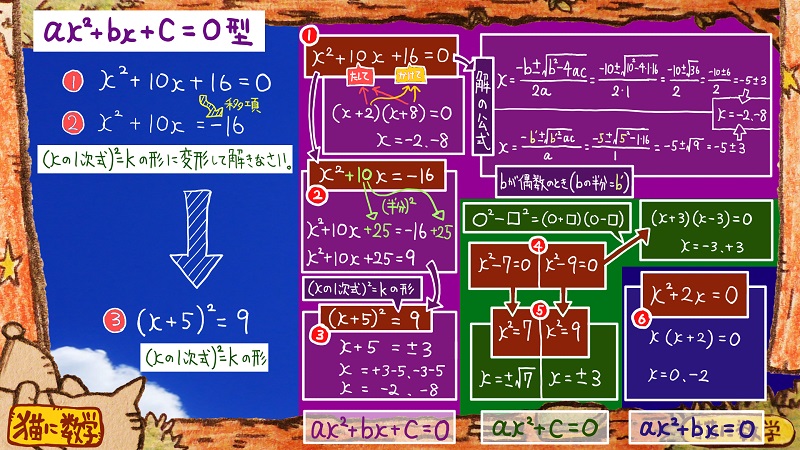
最後になりましたが、解法のパターンとして
一番ややこしい手順を紹介します。
①やそれを変形した②から
③の形に変形して、平方根の考えかたを使って解く
という手順になります。
この方法は正直めんどくさいと感じる方もいると思いますが
教科書に登場しているので仕方がないです。
あとは、高校数学で必要になる平方完成という変形の練習になってるので
まあ計算問題の一種と割り切って練習しておきましょう。
白い囲みに書いてあるように
「(xの1次式)の2乗=kの形に変形して解きなさい。」
という指示があれば今回の手順を使います。

まず、x係数にあたる10に注目します。
この10を半分にします。
5になりますね。
そして、その5を2乗します。
25ですね。
それを、方程式の右辺にも左辺にも加えます。
もともと右辺と左辺はイコールが成り立っていた方程式ですよね。
その右辺と左辺にそれぞれおなじ25を足すので、出来上がった方程式のイコール関係は相変わらず成り立っていますよね。
25を足した左辺の部分は因数分解できます。
公式が小さく書いてありますが
この公式は別に覚えなくても変形することはできます。
さっき、かけて16になる数字とたして10になる数字を探して
(x+2)(x+8)というように因数分解した話を覚えていますでしょうか?
別にこの方法を使って因数分解してもいいのです。
ちょっとやってみましょう。
この場合は
かけて25になって、たして10になる2つの数字を探すことになります。
かけて25になる数字から探したほうが、見つけやすいです。
どうでしょうか?
5と5という組み合わせが見つかりましたでしょうか。
これで
(x+5)(x+5)という形に因数分解できましたね。
これで③の形に変形することができました。
あとはすでに説明した③の方法で解けばOKということですね。
因数分解を利用した二次方程式の練習問題を無料プリントでどうぞ
長々と説明しましたが、一応これで中学数学で習う二次方程式の解法の全パターンを網羅できたかと思います。
ここまでシンプルで簡単な例題で説明してきましたが、
ここからは、ちょっとだけひねったレベルのものも混ぜながら、定期テストに出題されそうな問題に慣れてもらおうと思います。

まずは復習です。
これは①のパターンですので、このまま因数分解できるかどうかを試すのがいいでしょう。
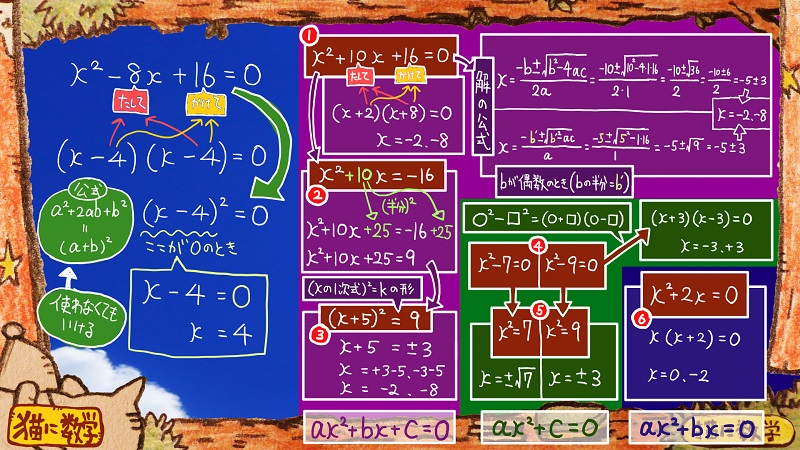
このように、かけて16、たして-8になるような2つの数字を探します。
-4と-4ですね。
(x-4)(x-4)=0になりますね。
同じものを2回掛けているので左辺は
(x-4)の2乗
というように短く書き直すことができます。
あとはご覧の通りで
x=4になります。

次はこの2問です。
どうでしょうか?
わかりましたでしょうか?

上の問題は最初から因数分解されていて右辺が0なので、答えまであと少しという状態になっています。
カッコのなかが見たことのない形になっていて戸惑う方もいるかも知れませんがやることは一緒です。
(1-x)の部分が0のとき、(3x+1)がどんな数字になっていても
そこに0が掛かるので、イコールゼロという方程式が成立しますよね。
なので、(1-x)が0の場合は、xが何であればいいかを計算すればいいことになります。
つまり、1-x=0という方程式を解いてx=1ということになりますね。
これが解のひとつです。
もうひとつも同様に考えます。
(3x-1)の部分が0のときだったら(1-x)がどんな数字であったとしても
そこに0がかかることになるので、イコールゼロという方程式が成立しますよね。
なので、(3x-1)が0の場合は、xが何であればいいかを求めることになります。
よって、3x-1=0を解いて、x=マイナス3分の1ということになります。
これで二つ目の解がでましたね。
続いて下の問題を見てみましょう。
まずこれは、右辺に5xがあって見にくいので、左辺に移項します。
するとこれは青色のゾーンにある⑥の解法パターンだということに気がつくと思います。
あとはさっきと同じように解いてください。

次はこの問題です。
これは、解の公式を使って解く方法もありますが、せっかくなので工夫して解く方法を解説します。
定期テストにも「工夫して解け」みたいな問題も出る可能性もありますので、必要な方はご覧ください。

まず、右辺の項をすべて左辺に移項させて右辺を0にします。
xの2乗の係数である50が大きいので、もし解の公式を使うとしたら計算が大変そうだなあと思います。
なんかコレ、小さくできないかなあと観察してみます。
すると左辺の項がすべて2の倍数になっていることに気がつきます。
50も-20も2もすべて2の倍数ですよね。
なので両辺を2で割ります。
左辺に登場していた数字はすべて半分になりました。
右辺は0を2で割ったので依然として0のままです。
式が簡単になったのでここで二次方程式の解の公式を使うのもありです。
ですが、今回はここから工夫する方法をご紹介します。
まず25という数字が5の2乗になっているということに気がつく必要があります。
これに気がついたら25xの2乗という項が5xの2乗だということがわかります。
そして見やすいように5xをXに置き換えて表現を変えてみます。
すると、ご覧のような式が現れました。
Xの2乗-X+1=0ですね。
これは因数分解できるので
因数分解すると、結局
(X-1)の2乗=0になります。
そこで
Xを5xという表現にもどします。
あとは
(5x-1)の部分が0になるときのxを求めて答えを出すということですね。
さて、続いてこちらの問題ですが
解き方に注文をつけています。
平方根の考えを使って解きなさいとありますがどうでしょうか?
右の表のどのパターンの問題だったか思い出せるでしょうか?

左側のふたつの問題は④を⑤に変形して解く問題。
右側のふたつの問題は③の問題でしたね。
また、下の二つの問題は分数の形でルートが登場するという形になっています。
このあたり、ややこしいと感じる方が多いと思ったので練習問題として登場させておきました。
それでは次で最後の問題です。

中学で習う二次方程式の解き方を総復習できる柔軟な問題です。
右の表を見ながらできるだけ多くのパターンで解いてみましょう。
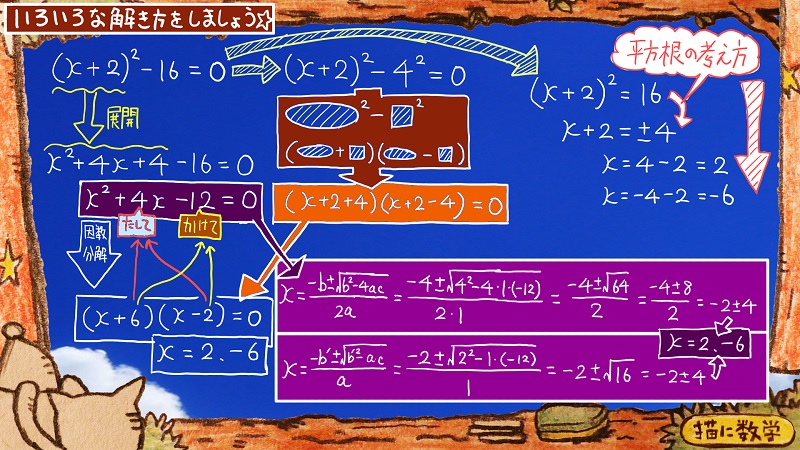
どうでしょうか?
ここには4パターンの解き方が書いていますが、どれだけ解答できたでしょうか?
解の公式はbが偶数だった場合の計算も書いていますので、これも含めると全部で5パターンですね。
「猫に数学」の公式サイトには、今回登場した問題をPDFにして無料でダウンロードできるようにしてありますので、手を動かして練習したいという方はどうぞプリントアウトして使ってください。
あと今回のパターンをもっといろいろ練習したいとか、公立高校入試の最初の計算問題なんかもリクエストがあれば登場させる予定です。
動画で解説をきけてプリントもダウンロードできるようにしようかと思っています。
なのでご希望があればリクエストお願いします。
以上、中学3年生の数学で勉強する、因数分解と解の公式を使った二次方程式の解き方について、解説とその練習問題でした☆
次回は「たすきがけ」による因数分解を利用した、少し難しめの二次方程式を解く方法について解説します。
ご質問がありましたら、YouTube授業動画のコメント欄に記入いただけると、僕の時間の許す限りですが、返答させていただきます。