正の約数の個数と総和を求める公式の解説

題材：オリジナル問題：正の約数の個数と総和	難易度：★☆☆☆☆☆☆☆☆☆

こんにちは、坂田です☆

今回は、正の約数の個数とその総和、についてオリジナル問題で解説します。

この例題は、教科書レベルや白チャートや黄色チャートの基本レベルなので、定期テスト対策などで困っているかたにも存分に利用してもらいたいと思います。

それではさっそく問題を見てみましょう。

題材：正の約数の個数、約数の総和	難易度：★☆☆☆☆☆☆☆☆☆

この問題、公立高校の標準レベルの高校数学であれば、数Ａの教科書の「場合の数」という単元で、１学期に遭遇するテーマです。

高校１年生の数学のなかで、最初に結構つまづきそうな内容なので、今回はこのテーマ（約数の個数と約数の総和）を扱います。

また、高校入試において、数学の難問を課す私立の受験対策にとっても必要になってくる単元です。

公式をそのまま暗記して使っても良いのですが、できれば理解できていたほうが、忘れても自力で思い出せるので、説明をご覧いただければと思います。

じゃあ問題を解いていきましょう。

まず、正の約数の個数、について考えていきますが、問題の意味がわからない方のために（１）は、答えを先に見てもらいますね。

こんな感じですね。

１８の約数はこのように、

１、２、３、６、９、１８、と

６個あります。

正の約数の個数を求めよ、というのは、この個数を聞かれていたということですね。

まあ、この問題のように、１８という小さな数字だったらこんな風に一つひとつ書き出していけば解答することも簡単です。

けれど、たとえば（３）の７２０のように、数字が大きくなってくると、それもなかなか難しくなってしまいます。

そんなときのために、解き方の手順を身に付けましょうということが今回のメインテーマです。

なので、正の約数の個数が６個ということはわかっているんですが、これを計算によって導き出す手順と、その説明をこれからご覧いただこうと思います。

正の約数の個数を求める公式の解説

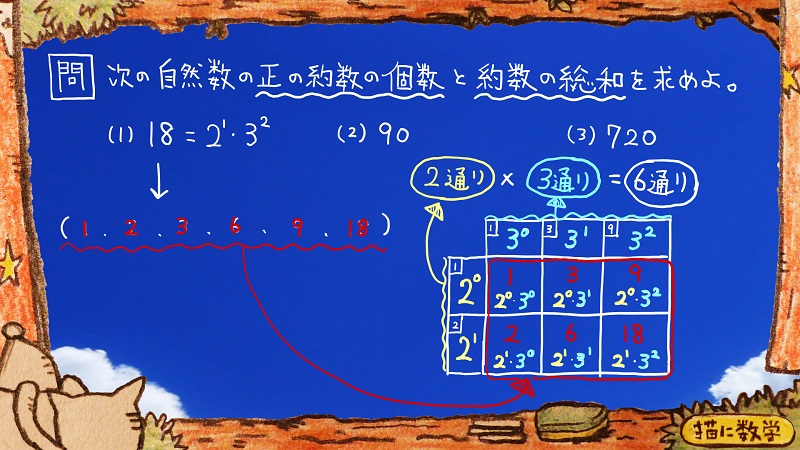
まず、１８を素因数分解します。

１８という整数は２×３×３という素数の掛け算で表現ができます。

２が１個

３が２個

あるわけですが、例えばこのなかから２を１個、３を１個選んで掛け算をしてみます。

２×３で６になりますね。

この数字は

１８の約数である

１、２、３、６、９、１８のなかにありますね。

では、２を０個、３を２個、選んで掛け算をしてみます。

３×３で９ですね。

そして、これも１８の約数のなかにちゃんとありますね。

このあたりで、右下の表の意味が、ちょっとわかってきた方もいると思います。

表の縦マスには、

黄色で２の０乗と２の１乗が

表の横マスには

水色で３の０乗と３の１乗と３の２乗が

ならんでいます。

この「なんとか乗」という部分の数字のことを指数と言うのですが

指数が０のときは、さっきの話で言う「０個選んだとき」というように考えてください。

たとえば、縦マスで２の０乗をチョイスして、横マスで３の２乗をチョイスした場合は

さっきそうしたように、２を０個、３を２個選んで掛け合わせたと思ってほしいのですね。

ちょうどその該当するマスには、赤色で９と書かれていますよね。

つまり、縦２マスかける横３マスで構成される、表にある６マスのなかには、１８の約数である６個のすべてのパターンが網羅されているということが、これでおわかりになるかと思います。

２通り×３通り＝６通りと書かれている部分は、この６マスという数を計算する工程を説明したものだということが理解していただけるでしょうか。

注意していただきたいのですが、２通りというのは素因数の２を表わしたものではなく、

２の０乗

２の１乗

という２パターンを表わした２という数字です。

３通りというのも、素因数の３を表わしたものではなくて

３の０乗

３の１乗

３の２乗

という３パターンを表わした３という数字です。

ちょっとこのあたり、わかったようなわからないような感覚になる方もいると思います。

そんな場合は、とりあえず問題が解けるようになることを優先してください。

計算方法が身についてから、本質を理解したいという場合は、もう一度この説明を見てもらったほうがいいでしょう。

答えの求め方ですが、こんな表をいちいち書いて求めるのは大変ですね。（こんな風に最初に理解するためには必要だったりしますが…）

「縦２マスで横３マスだから、約数の個数は、２かける３マスの合計６マスだから６個だね！」

と考えてもいいのですが、それよりも手っ取り早い計算の方法を覚えてしまいましょう。

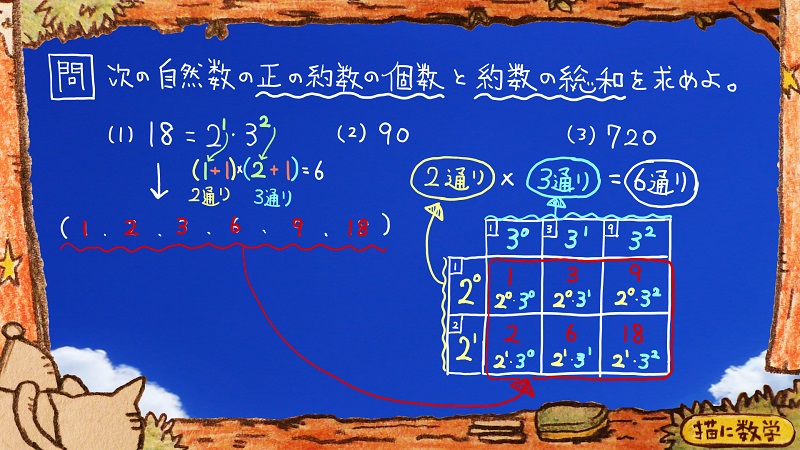
結局は１８という数字から

２通り×３通り

という式を導きだせればいいですので、このあたりの手順を公式のように身に付けていきましょう。

１８という数字を素因数分解すると

２の１乗×３の２乗という表現にかえることができましたね。

それから

２の指数である１乗という情報から

２の０乗と２の１乗という２パターンが縦マスに登場しました。

また

３の指数である２乗という情報から

３の０乗と３の１乗と３の２乗という３パターンが横マスに登場しましたね。

結局この指数にプラス１した数字が、縦マスと横マスの数になっているわけです。

なので、

１８を素因数分解して、２の１乗×３の２乗という表現に変えたら

１乗にプラス１した２と

２乗にプラス１した３という数字を

掛け合わせれば

さっきの

２通り×３通り＝６通りという

計算をしたのと本質的に同じ工程になります。

最初のうちは慣れないかもしれませんが（２）（３）と練習と慣れを重ねるにつれて、徐々に簡単に感じていきます。

なのでできれば、（２）と（３）は実際に紙とペンを使って問題を解いてみてください。

約数の総和を求める方法

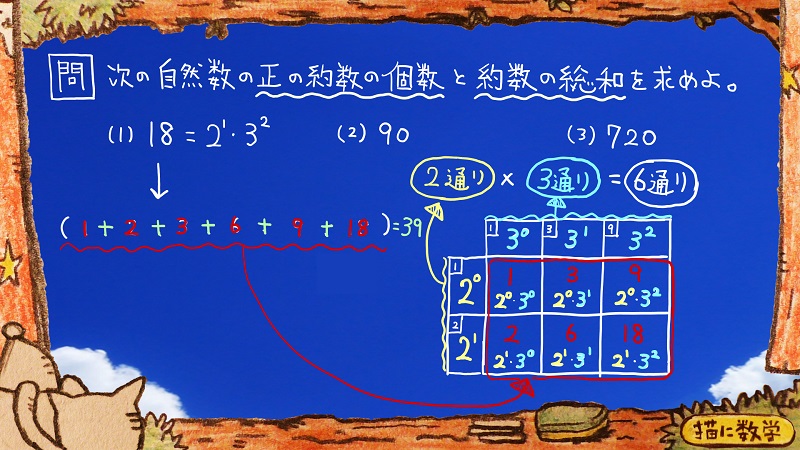
次に「約数の総和を求めよ」という問題ですが。

これも問題の意味をまず把握するために、最初に答えを表示しておきます。

１８という数字のしたに６個の約数がならんでいますね。

総和というのは、すべて足した合計の値のことです。

なので

１、２、３、６、９、１８という数字をすべて足してゆきます。

合計で３９ですね。

総和を求めよ、というのは、これをたずねられていた訳です。

これも１８という数字だったので、このように書き出して求めるのも全然アリなんですが（３）でこれをやると大変です。

なので、約数の総和を求める式を導き出す手順を身に付けていきましょう。

赤色で書かれた１８の約数が６個ありますが、その下にこのようなものを書き足してみました。

例えば赤色で書かれた１の下には

２の０乗×３の０乗という表現に変化しています。

ちょうど右側の表にある赤色で書かれた６個の約数の下の部分を見てみてください。

そこの部分に書いてある表現に、それぞれ置き換えられているということです。

表現が変わっているだけで、この６個の数字をすべて合計しても、先程と同じように３９という答えになります。

そして、「展開」と書かれている矢印があるかと思いますが、矢印の下の式を展開すると、ちょうど矢印の上の式になりますよね。

下の式で茶色の矢印が６本ありますが、

ちょうど２つの項と３つの項が掛け合わさって上の式へと展開されます。

すると６つの項が足し算のかたちでならぶというようになっていますね。

つまり、展開される前にあたる下の式を計算しても、その答えは上の式と同様、３９という同じ値になるハズですよね。

この式を展開して計算すると上の式を計算することになります。

それよりも、

２の０乗である１と

２の１乗である２を

合計して３にします。

そして

３の０乗である１

３の１乗である３

３の２乗である９を

合計して１３にします。

結局この式は

３×１３ということになって

それを計算すれば簡単ですよね。

つまり、ここで身に付けないといけないのは

展開させる前の式を作り出す手順ということになります。

これは（２）と（３）の問題でまとめて説明していきますので、とりあえずここまで理解できたら、次の（２）に進みましょう。

（２）自然数９０の正の約数の個数は？

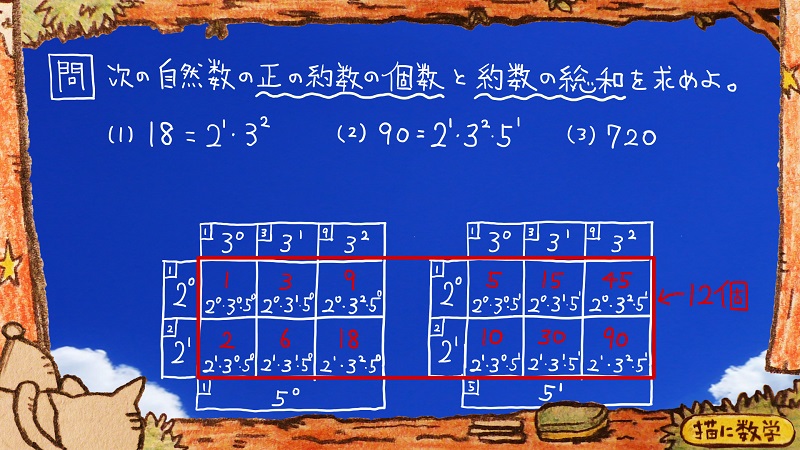
（２）ですがまず、約数の個数を求めてみます。

さっき違う話をしていたので、イメージを思い出すために表も書いておきました。

自然数９０を素因数分解すると、

２の１乗

３の２乗

というところまでは（１）と同じなのですが

５の１乗

がよけいに増えていますね。

この三種類の数字を使うと

下の表のように１２個のマスができます。

赤色で書かれている数字が９０の約数ですね。

全部で１２個あるので、９０の正の約数の個数は１２個あるということになります。

さあこれを式をつくることで求めてみましょう。

表を見ればわかるのですが、この１２個という数字は

黄色の２通り×水色の３通り×紫色の２通り

をすればいいということが視覚的にわかるかと思います。

この２×３×２という式は

９０を素因数分解した式にある

２の１乗の１

３の２乗の２

５の１乗の１

という指数に対してそれぞれプラスした数字を掛けたもの、ということになります。

ちょっと思い出したでしょうか？

この感覚を持った今の状態で（３）も解いてみましょう。

（３）は７２０という数字ですね。

この正の約数の個数を求めようとしたら、まず７２０を素因数分解します。

７２０は、

２の４乗

３の２乗

５の１乗

がでてきました。

このなかから指数である、４、２、１をとりだして、それぞれプラス１します。

それをすべて掛け合わせた値が、約数の個数にあたるのでしたね。

ということで７２０の正の約数の個数は３０個、ということが判明しました。

９０と７２０の約数の総和

最後に（２）と（３）の約数の総和を求めて終りにしましょう。

（１）の問題の、下のほうにある、茶色の矢印が６つ付いている式を見てください。

約数の総和を求めるときは、この式をつくることを身に付けよう！

という説明のところで話がストップしていたと思います。

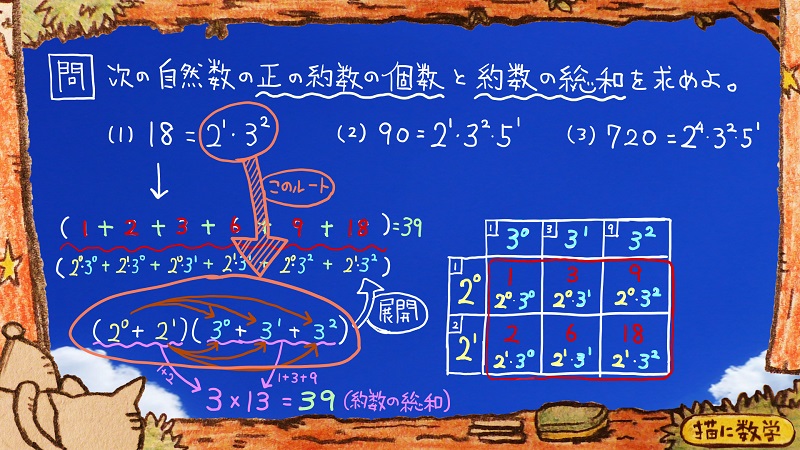
この式へとたどり着く手順ですが、まず１８という自然数を素因数分解して、そこから下の式を作ることを考えるのが無駄のないルートになります。

勘のいい方は、もうこの段階でわかるかもしれませんね。

１８という自然数を、２の１乗×３の２乗というカタチに変化させ下準備します。

２の１乗ということなので、２の０乗から、２の１乗になるまで足したものを用意します。

この場合は、２の０乗＋２の１乗ですね。

３は２乗まであるので、３の０乗から、３の２乗になるまで足したものを用意します。

この場合は、３の０乗＋３の１乗＋３の２乗ですね。

そして、用意したふたつを掛け合わせた式が「約数の総和を求める式」ということになります。

この要領で（２）（３）もまとめて式を作ってみましょう。

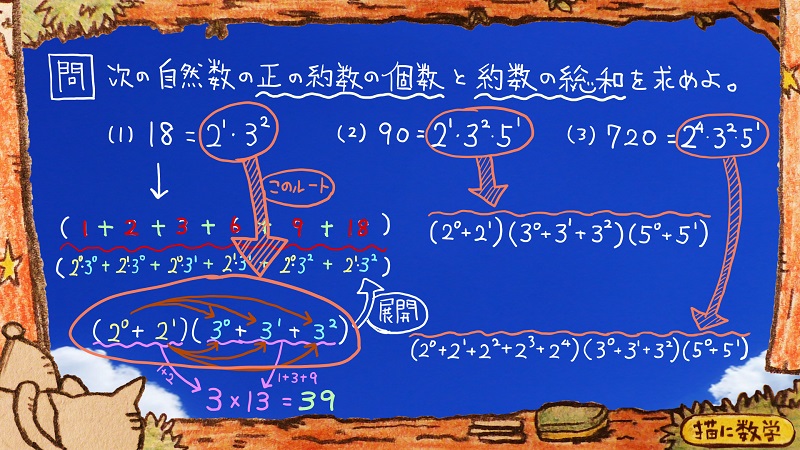
どうでしょうか？

このようになりましたでしょうか？

こうなったら、あとはこのように計算をしてゆくだけですね。

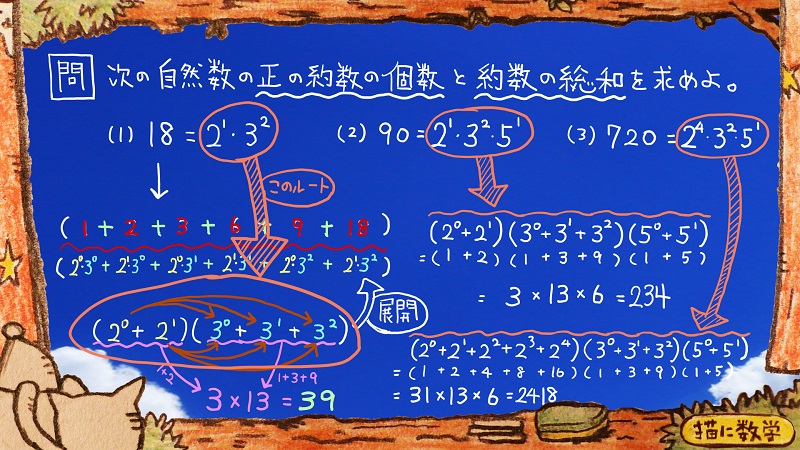
どの問題もそうですが、とく手順を知ったら、何度か練習して慣れるための時間をとるだけで、どんどん簡単になっていきます。

定期テスト対策の準備をするときなんかも、こんなふうに、慣れない工程だけ再現する練習というのをやってみることをおすすめします。

解き方は理解していたハズなのに、テスト本番で思い出せなかったという方も多いと思います。

数学って、スポーツと似ているところがあって、ルールだけ学んでもうまくはならないんですね。

解くパターンを知ったら、それを再現できるかどうかの練習というものを繰り返して慣れる必要があります。

理解する時間よりも、この時間こそが、数学を身に付けるトレーニングの時間だと思ってください。

考えて解くことが重要になってくるのは、思考力が関わってくる難問の対策をしたい場合です。

なので、この問題も、まずは練習して慣れてほしいと思います。

以上、自然数の正の約数の個数とその総和を求める問題の公式を解説しました。

おつかれさまです。