高校入試数学の相似な図形の応用問題を超難問で!洛南高校の過去問を解説
 |
|
| 題材:洛南高校、相似の問題 |
難易度:★★★★★★★★☆☆
|
こんにちは。坂田です★
今回は、相似な三角形が登場する高校入試の応用問題を解いてもらおうと思います。
かなり難しいですが、非常に重要な性質が登場するので、難関を受験される方は、相似な図形が登場する一つのパターンとして経験しておいてくれればと思います。
それでは、まずは問題を見てもらいましょう。
2016年に洛南高校の数学入試問題(過去問)の最後の大問5に登場した、相似の問題です。
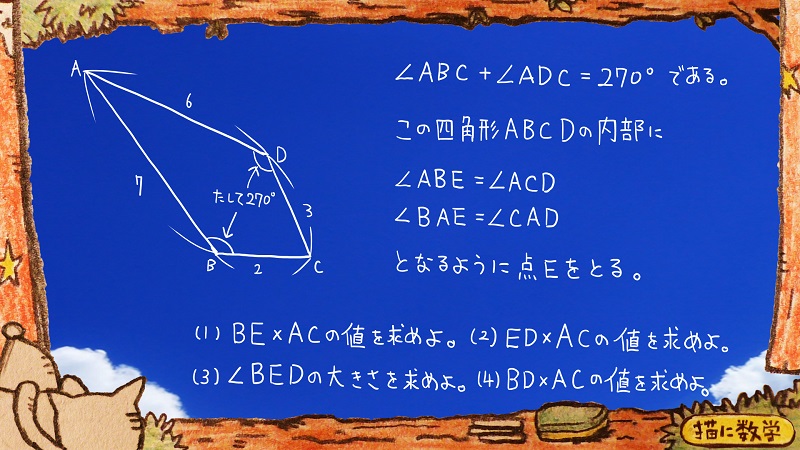 ∠ABC+∠ADC=270°とする。 ∠ABC+∠ADC=270°とする。
また、 ∠ABE=∠ACD となるように (1)BE×ACの値を求めよ。 (2)ED×ACの値を求めよ。 (3)∠BEDの値を求めよ。 (4)BD×ACの値を求めよ。 |
|
| 引用:洛南高校:2016年(平成28年)相似の性質 |
難易度:★★★★★★★★☆☆
|
まずこれは、最初の仮定で説明されている点Eの位置を想定するところから準備していきましょう。
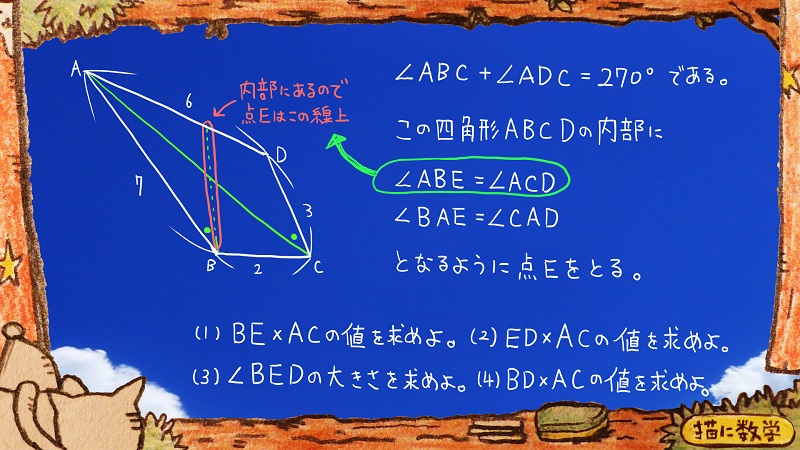
仮定のなかに
∠ABE=∠ACD
という条件があるので
青色の線上に点Eがあるということがわかります。
それからもうひとつの条件
∠BAE=∠CAD
にしたがって点Eを定めると
以下のようになります。
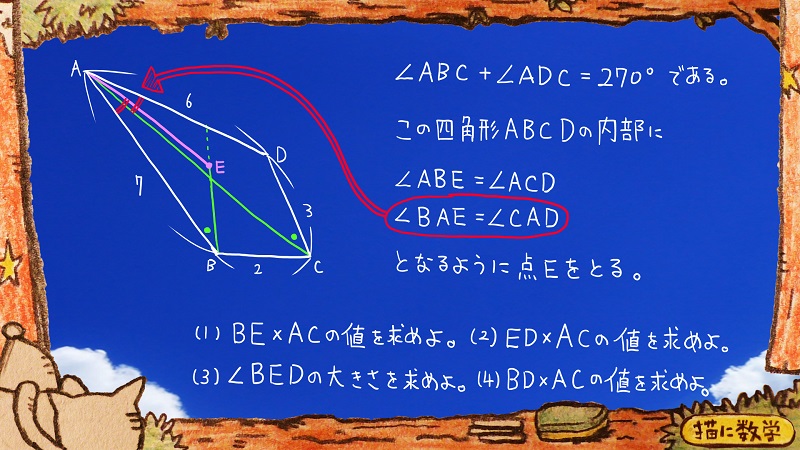
ひょっとしてこんな図を想定された方がいるかもしれませんが
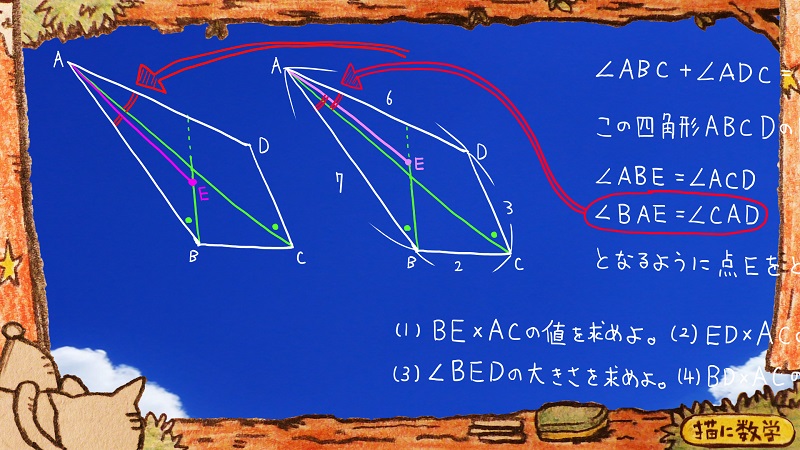
これでも解法は変わりません。
洛南高校の数学過去問(1)BE×ACの値を求めよ
さて、題1問目ですが、どうやって解けばいいのか、最初の図方からはわかりにくいかもしれません。
まず、様子を観察してみると、2つの三角形が互いに相似な図形であることが見えてきます。
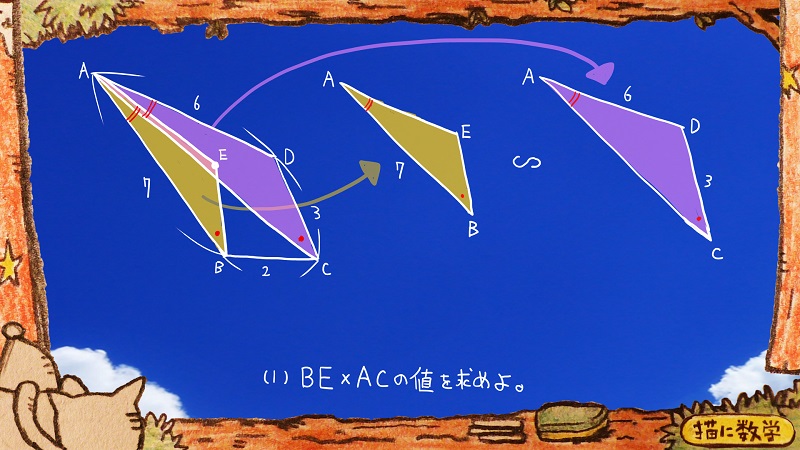
対応する2組の角度が互いに等しいからこの2つの三角形は相似ですね。
で、ここからどう考えるかですが、この状態で適当にあれこれやっていても解答できることも大いにあると思います。
相似であるということから、問題に関わっているBEとACを登場させた式を導き出すとこのようになりますよね。
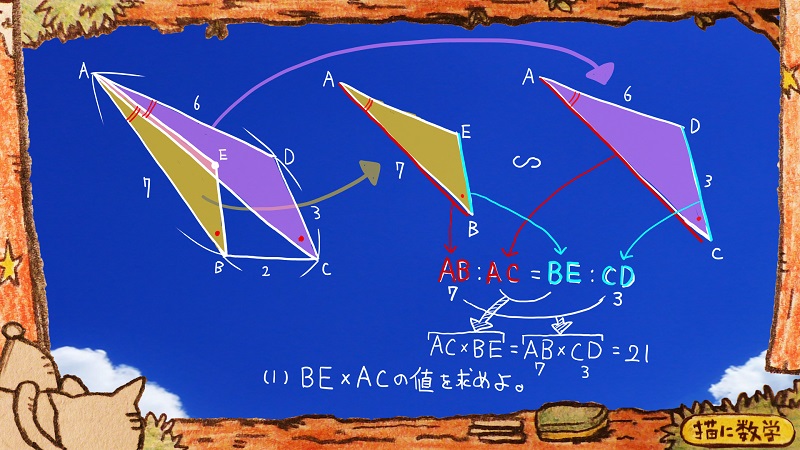
このようにして、BE×ACの値を求めることができるのですが、いちおう簡単な例題でこのパターンをなじませておきましょう。
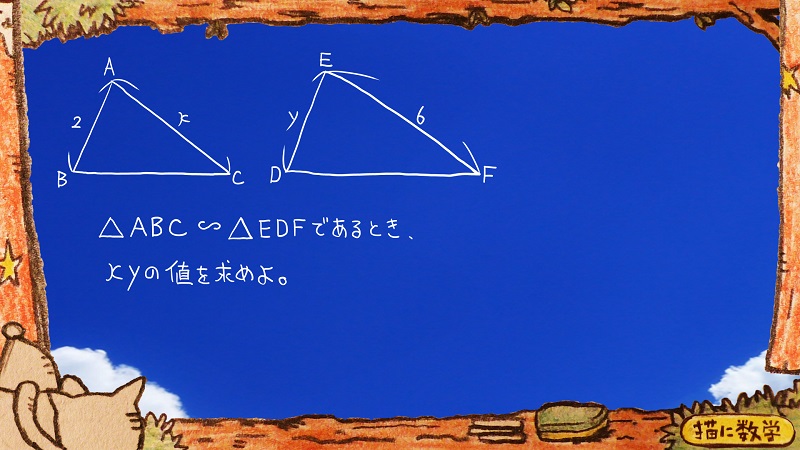
相似の性質を利用した問題
 |
|
| 題材:オリジナル問題 |
難易度:★★☆☆☆☆☆☆☆☆
|
これもさっきと同様、問題に関わるxとyを登場させると解答が導き出せます。
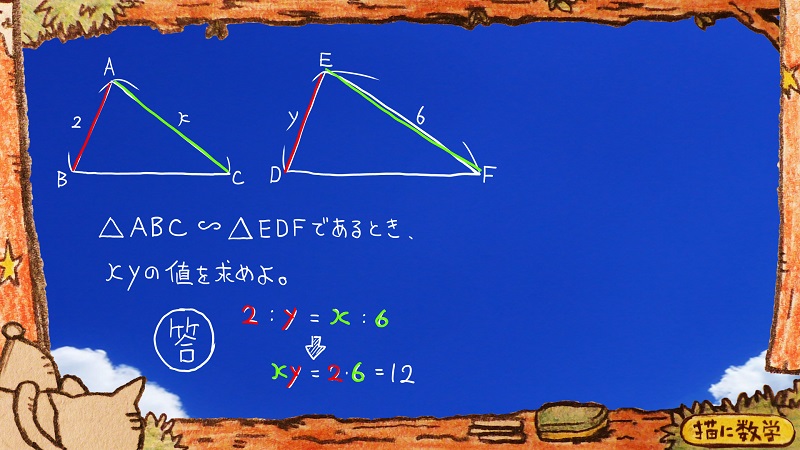
このパターンに慣れてきたら即座にxy=2×6とイメージすることができます。
感覚としてはこんな図がわかりやすいかもしれませんね。
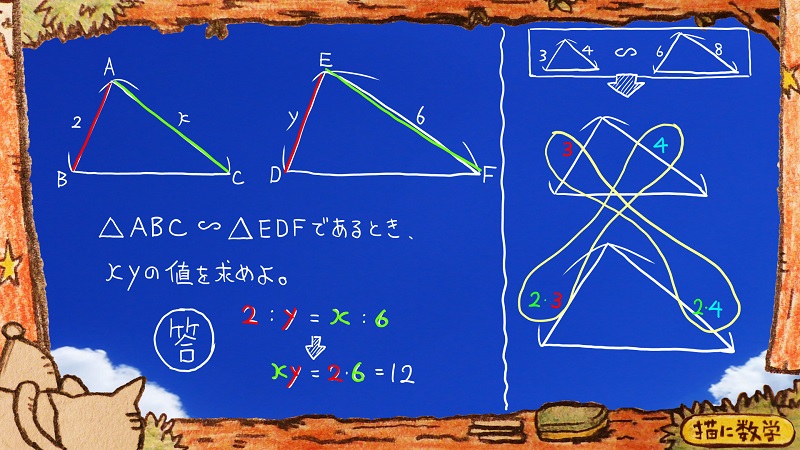
上の三角形と下の三角形が相似だとして、このように対応しない辺同士を掛け合わせます。
すると、どちらも赤色、水色、緑色の三色がかけあわされることとなり、値が同じになります。
この感覚で左の問題を眺めてみると結構簡単に感じるのではないでしょうか?
さあ、それじゃあ、洛南高校の入試問題(過去問)も、もう一度見てみましょう。

互いに対応しない辺を掛け合わせる感覚があれば、この状態でのタイムロスはなくなるハズです。
では次の問題に行ってみましょう。
洛南高校の数学過去問(2)ED×ACの値を求めよ
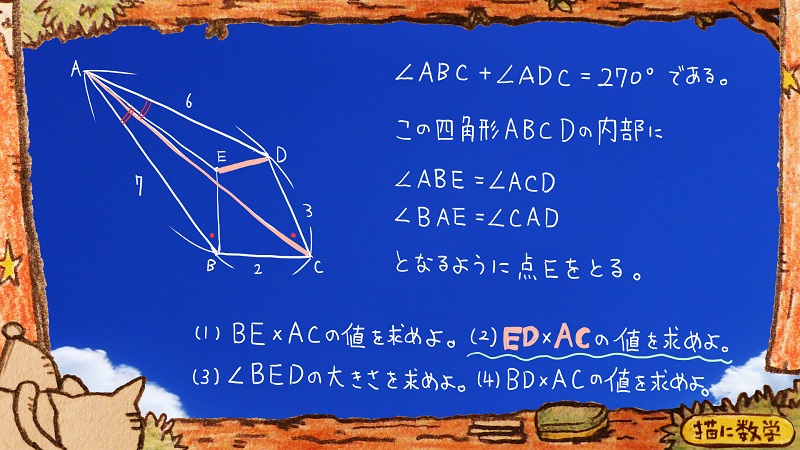
辺ACが登場するのはさっきの問題と同じなのですが、今度は辺EDを新たに登場させないといけません。
もしもこれが(1)と同じ要領で値を求めさせる問題だとするならば、ここで辺EDを持つ三角形を登場させなければいけません。
辺DEが関わる三角形といえば、普通に考えれば△AEDでしょう。
補助線を引いて△CEDを考えるよりも、前者のほうが道がひらけていそうですね。
というのも、仮定としてある∠BAE=∠CADを意識すると、このようになるからです。
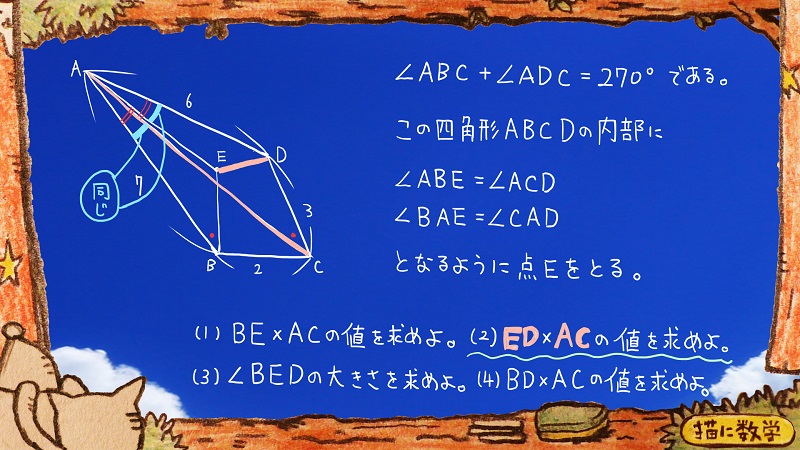
∠BACと∠EADが同じになりますよね。
そして、問題に登場しているEDとACを合わせて意識するとどうでしょうか?
このように、
ふたつの三角形が浮かびあがってこないですか?
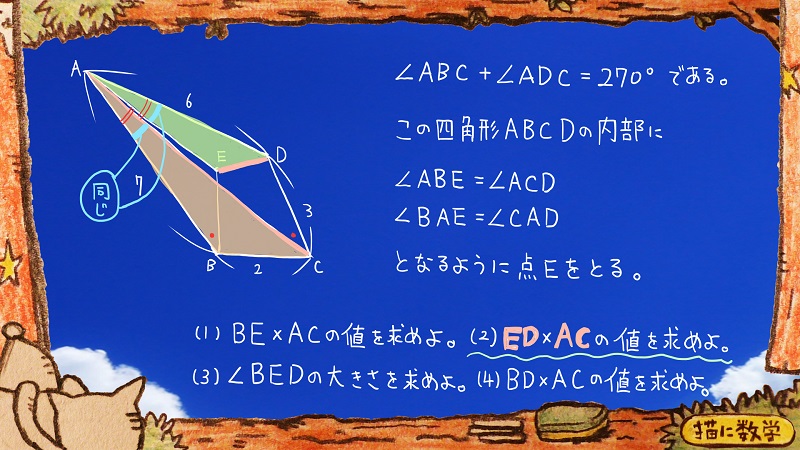
もしもこの三角形が相似だとするのなら、このように答えは導き出せそうですね。
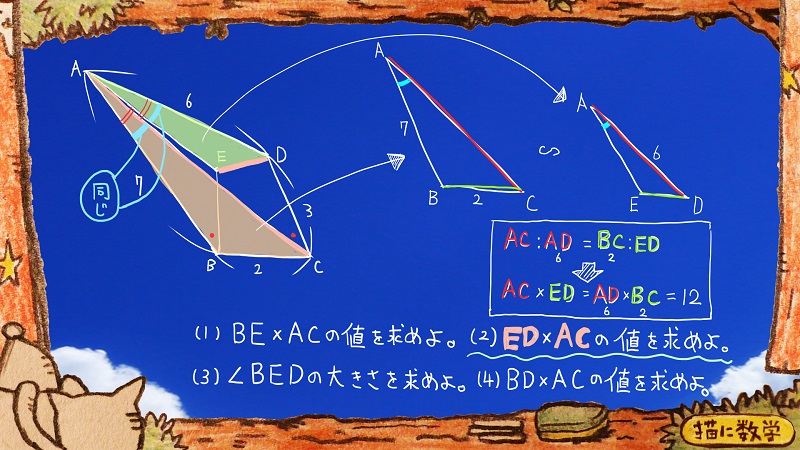
さて、この2つの三角形は果たして相似なのでしょうか
ここでちょっと脱線して、相似な三角形2つで成り立つ性質の話をしようと思います。
相似な2つの三角形から、相似な三角形が生まれるパターン
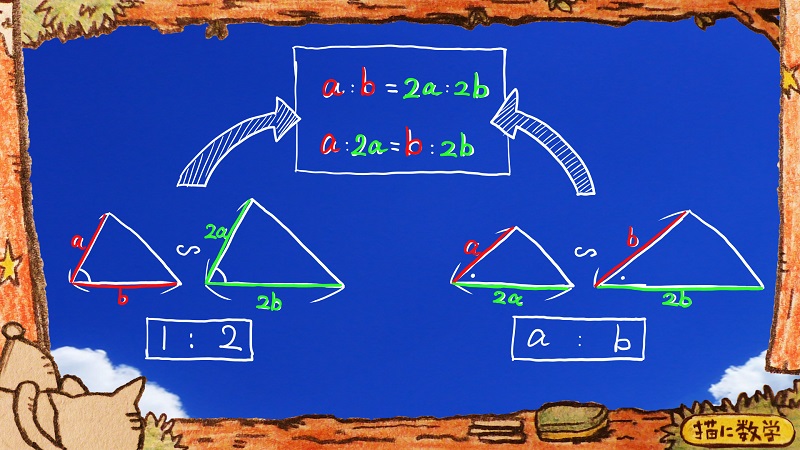
これは相似な三角形のペアを2通り並べたものです。
この二つのペアの三角形は使用している辺の長さを、ご覧のように入れ替えただけですが、同じ比例式を導くことができます。
左のペアは辺の比が1:2で
右のペアは辺の比がa:bになっていますね。
つまり、辺の比に関しては、このようなパターンだった場合、証明の道具とすることができるということですね。
ちょっと何を言ってるのか分かりにくいと思いますので、具体的に問題にしてもう一度説明しますね。
例えばこれがこんな問題になっていたらどうでしょうか?
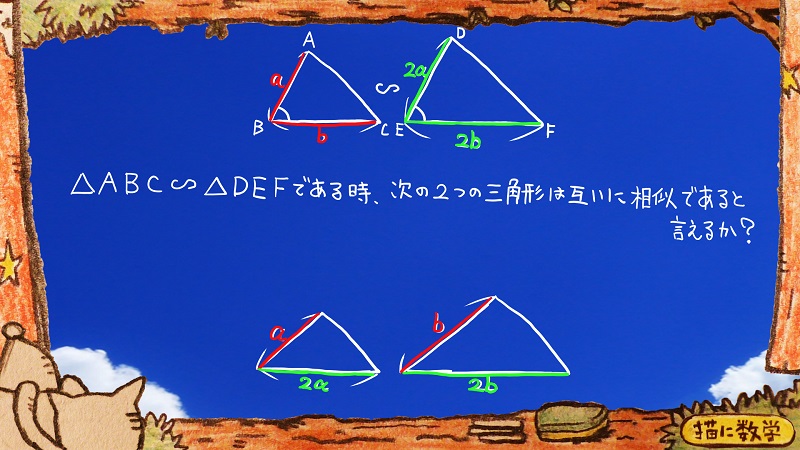
まず仮定より、
a:b=2a:2b
ということが導けます。
さっきの話でもありましたように、問題になっている三角形は、この比例式によって、「二組の辺の比が等しい」ということだけは証明できます。
 |
|
| 題材:オリジナル問題 |
難易度:★☆☆☆☆☆☆☆☆☆
|
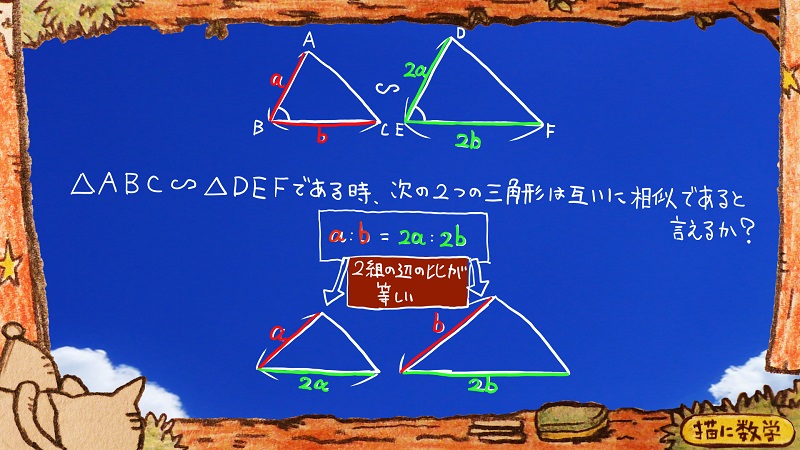
上の相似な2つの三角形は辺の比が1:2
下の2つの三角形は辺の比がa:b
どちらも
a:b=2a:2b
という同じ式で表現することができるからです。
証明の道具にすることができると言ったのはこういう意味です。
ただ、下の2つの三角形が相似であるということは、これだけでは証明できません。
二組の辺の比が等しいということまでは証明できたのですが、そのはさむ角度がそれぞれ等しいということが証明できなければなりません。
ゆえに、これだけでは不十分、ということになります。
たしかにこんな場合は相似でない、ということは明らかですもんね。

かなり回りくどい説明になっていますが、話を進めましょう。
さて、この上の三角形のペアをこのように二つ重ねてみます。
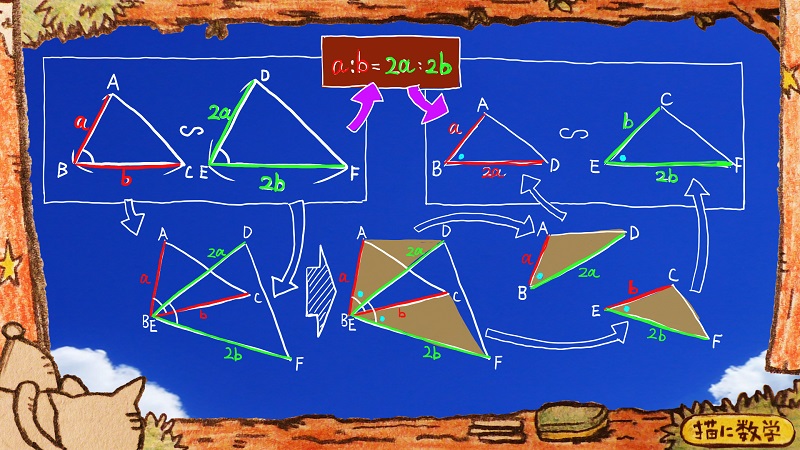
すると、オレンジ色の部分に二つの三角形が現れます。
これってとりだして、並べてみると、さっきの問題に出たもう一つのペアの三角形になっていますね。
辺の組みあわせは少なくとも同じパターンですよね。
そして、重なっているところの図を見てみるとわかると思うんですが、二組の辺の比だけじゃなく「そのはさむ角度も等しい」ということが明らかですよね。
なので、左側の相似な三角形のペアをこのように重ねて現れた、右側の三角形のペアも、互いに相似だということがわかるかと思います。
このように「相似な三角形を重ねて相似な三角形を登場させる」パターンが今回の洛南高校の数学で登場しているのです。
それではもう一度、過去問にもどってみましょう。
相似の性質を利用した高校入試問題の難問
(1)の段階でわかっている相似の三角形のペアがありましたよね。
これをさっきの要領で重ねたパターンとしてとらえていくと、この問題の事態が把握できると思います。
こんな感じですね。
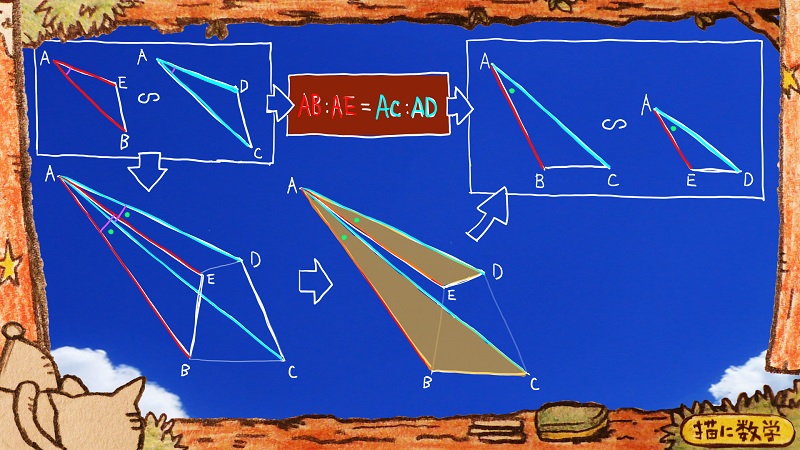
どうでしょうか?
左上にある2つの三角形が、(1)の段階でわかっている相似な三角形のペアです。
それを重ねると、黄色の部分にあたる図形が新たに相似な三角形のペアとして把握できるのではないでしょうか。
こうなると
あとは(1)を解いたのと同じ要領で解くことができます。
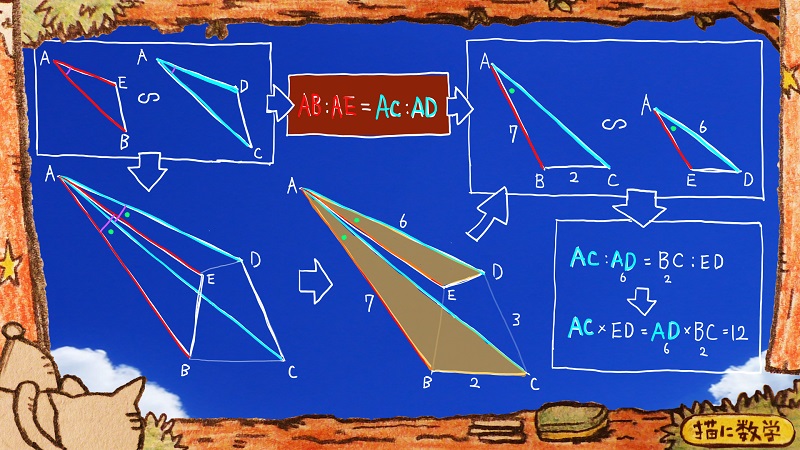
こうなりますね。
さあ、説明が大変長ったるくなっておりますが、次に行ってみましょう。
相似な図形の応用問題ってパターンに慣れていないと難しい
(3)∠BEDの値を求めよ。
これもいきなり入試問題に入る前に、ひとつの図で感覚を得てからにしましょう。
二つの相似な三角形を重ねた例の図です。
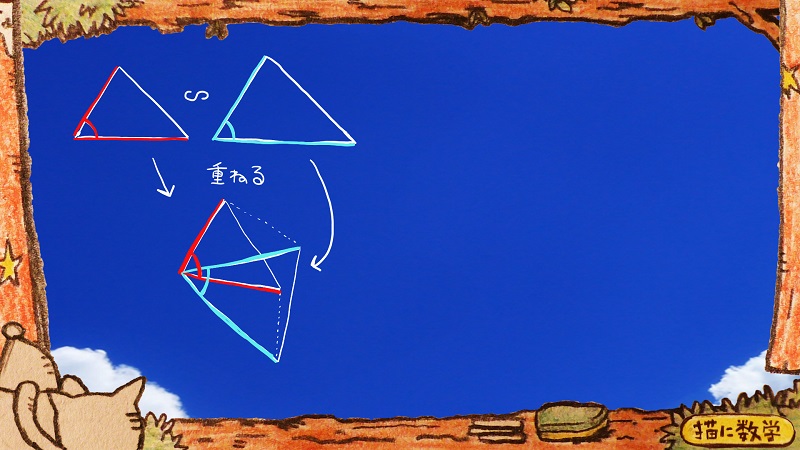
復習になりますが、ここで新たに相似な三角形のペアがこのように現れます。
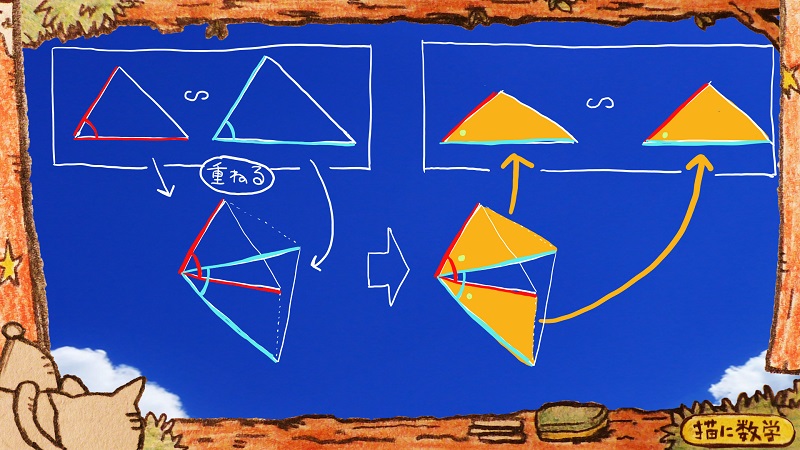
そして、ここに少し、角度に関する情報を付けたします。
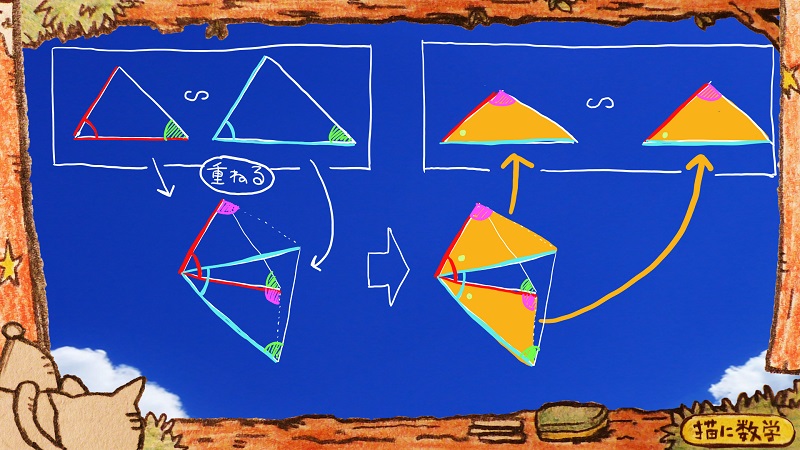
何をしたかと言うと、互いに相似な2組の三角形において、同じ角度に該当する緑と紫の部分を新たに書き示ました。
下の図ではそれがごっちゃになって書き込まれていますね。
たとえばこれで、この部分の角度がたして160度になっていた場合、真ん中あたりで「何度?」と聞かれている部分は何度になるでしょうか?
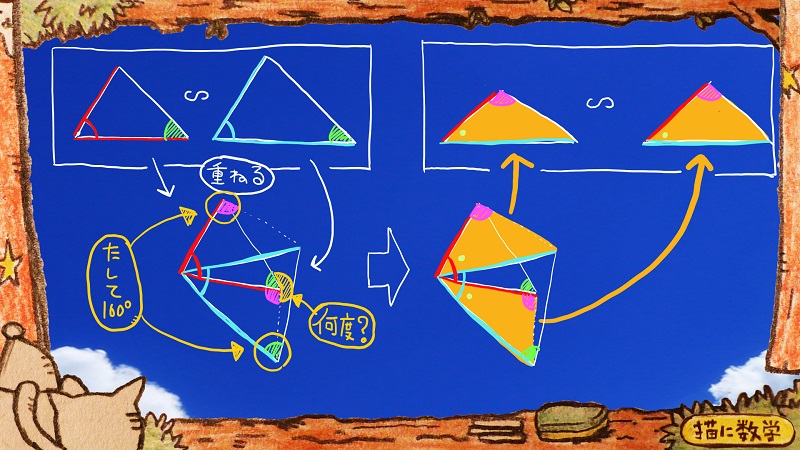
これはもうわかりますよね。
360°-160°で200°ですね。
これと同じ事態に今回の問題はなっています。
入試問題を見てみましょう。
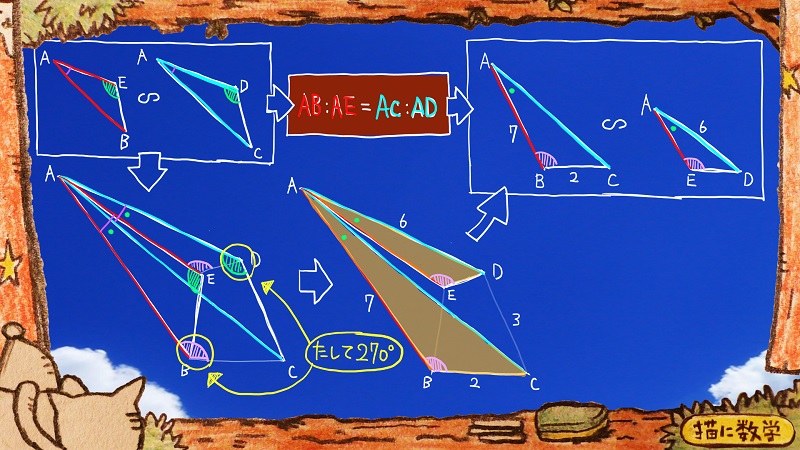
この書き込みを見るともうわかるでしょう。
問題文の仮定に、∠ABC+∠ADC=270°
とありますので、∠BEDは
360°-270°で90°ですね。
三問目もなんとか解くことができました。
さあ、それじゃあ最後の問題を解いてみましょう。
洛南高校の高校入試問題は難問だったの巻
(4)BD×ACの値を求めよ。
これまでの結果をすべて使う問題ですね。
まず、
(3)の結果が∠BED=90°ということで
直角三角形の斜辺にあたる辺BDが問題に関わっているナ、ということがわかります。
大問のなかの小問の連続は、誘導になっているパターンが多いので
じゃあ斜辺以外の辺BEと辺EDは(1)と(2)はなんか関連はないか?
と思って観察してみます。
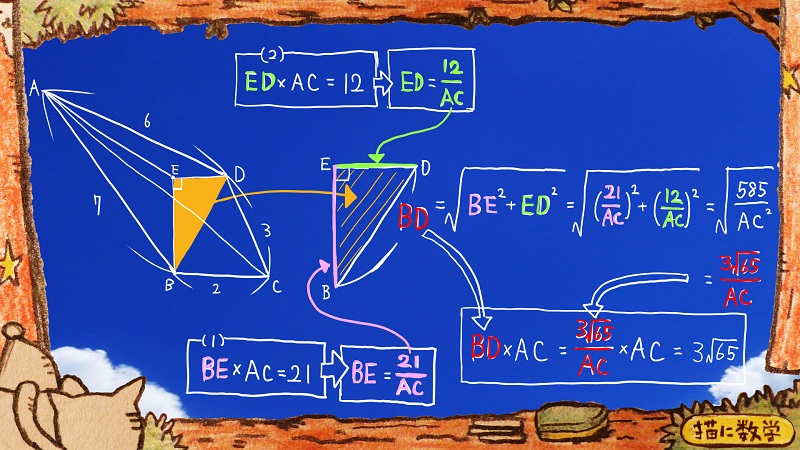
すると、どちらも、問題に関わる辺ACが登場しながら
(1)では辺BEが登場
(2)では辺EDが登場しています。
これらを変形すると
辺BEも辺EDもACを使って表現することができますね。
じゃあこのACによる表現のまま、三平方の定理で斜辺であるBDを表現すると
BDがACを使った表現になるじゃないか!ということがひらめけば最高です。
ここで、当初の問題である
BD×ACを、ACだけで表現しなおすと、ACが消えてくれて、値を求めることができるようになります。
以上、相似の入試問題の超難問でした
いかがでしたでしょうか?
最後の(4)はゴールからの逆算が非常に難しい問題だと思います。
特に、最後にACが消えるなんて、実際に計算してみなければわからない人もいると思います。
重要なことは、まず(3)の問題で90°という情報が出たことです。
問題に関わるBDが直角三角形の斜辺になっていることに、ピンとくる必要があります。
三平方の定理を使ってなんかするんちゃうか?
と勘ぐって、さらに
(1)(2)が誘導になってるんとちゃうか?
と考えてみなければ、解答へとたどり着くことは難しいでしょう。
ただ、この問題で学んでほしいことは(1)と(2)で登場した、相似な三角形を利用した性質にあります。
これは、ひとつの解法のパターンとして、何度か解いたり、自分で作ったりして、なじんでもらえたらと思います。
相似の応用問題である洛南高校の過去問の解説は以上になります
以上、相似の性質を利用した図形問題の難問を解説させてもらいました。
今回の洛南高校の過去問は、経験がないと結構手こずってしまうような、相似の性質を利用した問題ですので、何度か解いてみて、ぜひとも自分のものにしてもらえればと思います。





