灘高校の入試問題数学を解説

題材：灘高校	難易度：★★★★★★★★★☆

『猫に数学』は高校入試対策の数学講座です。

独学の難しい、ハイレベルな中学数学を動画授業でおとどけしていきます。

今回は、灘高校の整数問題の難問について、過去問を解説していきましょう。

整数問題は、高校入試数学のなかでも難問が比較的多く、因数にわけて考えるという視点が非常に重要になってきます。

因数や素因数への理解度が重要になってくる分野ですね。

問題や解法も様々なパターンがありますが、典型的な例題を一通りカバーするのがまずは得策でしょう。

今回とりあつかう問題は、数学的な思考力を試される難問ですので、何に気づき、どうやって解答へといたったのか、ということを特に注目しながら受講していただきたいと思います。

それではさっそく目標レベルの問題をご覧ください☆

灘高校の2016年（平成28年）の整数問題です。

灘高校の数学～2016年（平成28年）過去問の大問３

引用：灘高校：2016年（平成28年）	難易度：★★★★★★★★★☆

今回取り上げた入試問題は、灘高校2016年（平成28年）の過去問の大問３です。

大問３のなかに(1)と(2)がありますね。

そして(1)と(2)は、一見すると関連がなさそうに思えます。

けれどもこのような場合だと、(1)の問題は(2)の問題を攻略する上での誘導問題となっているパターンが非常に多いのです。

なので、まずは(1)を解説してから、その解法を(2)にあてはめてみようと試みます。

ちなみにこの問題は、あれこれと試行錯誤してから解説を視聴したほうが身につくので、今初めてこの問題に出くわしたという受験生は、ここで、10分からできれば20分ほど時間をかけてチャレンジしてみてほしいと思います。

(1)の解説

まずこの問題を見て、問題形式に戸惑った方もいるのではないでしょうか。

因数分解された左辺にはｘの式が、右辺にはｙの式があります。

この等式を満たしながら『ｘもｙも１桁の自然数』という条件に合うよう、ｘとｙに当てはまる数字を探せという問題です。

まず、この形式に慣れていない方のために、因数分解に関する問題を通して、この形式の整数問題にすこし慣れてから本題に移ろうと思います。

題材：オリジナル	難易度：★☆☆☆☆☆☆☆☆☆

この問題の攻略の糸口はまず、６の約数について考えます。

６の約数は１、２、３、６ですから、それらをｘｙに当てはめていった数字のペアが答えになります。

ちなみに、条件が『自然数』ではなくて『整数』であった場合、答えの数は２倍になりますし、

さらに、この関数をグラフにしてみると、このように、中学１年生で習う反比例のかたちだということがわかります。

このグラフ上に存在する格子点（ｘ座標もｙ座標もともに整数であるポイント）を数えていく問題でもあったわけですね。

グラフ上にはｘとｙのペアが無数に存在しますが、自然数や整数などという条件が付くと、因数の問題としてアプローチしたほうが手っ取り早いという問題の典型でしょう。

さあ、どんどんいきましょう。

次は、この問題を見てください。

題材：オリジナル	難易度：★☆☆☆☆☆☆☆☆☆

これは、中学数学の教科書レベルの問題です。

左辺が２つの因数に分解されていますので、かけて０になるということは、そのどちらかが０であればいいということになります。

ｘが０であった場合と（ｘ＋２）が０であった場合の２パターンにわけて考え、それぞれ求めていきます。

このように答えが求められました。

それでは右辺が０ではなくて、３だった場合はどうでしょうか？

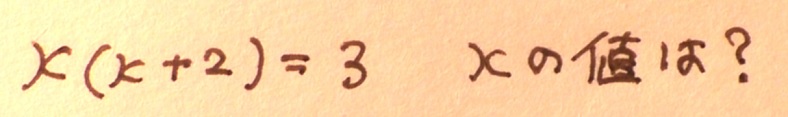題材：オリジナル	難易度：★☆☆☆☆☆☆☆☆☆

この問題を見たときに、ほとんどの中学生はこのような解答をすることでしょう。

これはまったく正しい解答であり、実際の入試問題においてはむしろこの解き方を採用することを強くオススメします。

けれども今回だけ、少し変わったアプローチで攻略してみましょう。

これまでの問題と同様、左辺を２つの因数として考えてみます。

２つの因数をかけあわせて３という右辺になるのですから、左辺の因数はそれぞれ３の因数ということになります。

このように答えの候補が４つ登場しました。

ただし、これは先ほどの問題と違い、左辺はｘしか文字が登場していません。

これはどういうことか？

書き出していった因数のペアを、詳しく見てみましょう。

（１、３）

（３、１）

（－１、－３）

（－１、－３）

この４つのペアが存在しますが、これはｘとｙのペアではなく

ｘと（ｘ＋２）のペアですね。

もしもこれが ｘｙ＝３ のように

ｘとｙのペアを求める問題であったら、

（ｘ、ｙ）＝（１、３）

（ｘ、ｙ）＝（３、１）

（ｘ、ｙ）＝（－１、－３）

（ｘ、ｙ）＝（－１、－３）

というように、解答することができます。

けれども今回は

（ｘ、ｘ＋２）＝（１、３）

（ｘ、ｘ＋２）＝（３、１）

（ｘ、ｘ＋２）＝（－１、－３）

（ｘ、ｘ＋２）＝（－３、－１）

というように対応させて考えています。

しかも因数のペアを先に書き出していっただけなので、そもそもｘが１のときに（ｘ＋２）がちゃんと３になるのか？などといった検証をしていかなければなりません。

というわけで、ひとつひとつチェックいきます。

まず（ｘ、ｘ＋２）＝（１、３）を検証します。

ｘが１のときに（ｘ＋２）はちゃんと３になりますね。

なので「ｘ＝１は解として採用」ということになります。

では（ｘ、ｘ＋２）＝（３、１）はどうか？

ｘが３のとき（ｘ＋２）は５になるので「ｘ＝３という解は除外」ということになります。

このようにして残りを検証していくと、このようになります。

（ｘ、ｘ＋２）＝（１、３）

（ｘ、ｘ＋２）≠（３、１）

（ｘ、ｘ＋２）≠（－１、－３）

（ｘ、ｘ＋２）＝（－３、－１）

よってｘは１の場合と－３の場合がきちんと、掛けて３になる因数のペアを生み出してくれるということがわかりました。

先ほどの結果と同じになりましたね。

実際にはこのような解き方はオススメできません。

なぜなら解が、今回のように必ずしも整数になるとは限らないからです。

例えばこのような問題は今の解き方はできませんね。

上記のように解の公式を使わなければ解答にたどりつけません。

ただし、『ｘは整数である』や『ｘは自然数である』といった条件があれば、このような考え方は非常に有効になってきます。

たとえばこのような問題が、今回の灘高校の問題に近いでしょう。

題材：オリジナル	難易度：★★★☆☆☆☆☆☆☆

まず『この問題の式のかたち』と『ｘもｙも１桁の自然数である』という条件を見たときに、因数の問題としてとらえられるかどうかということが非常に重要になってきます。

パッと見たときに、解き方がわからなくても、まずはこれまで同様、ｘが１から９までの場合をそれぞれ書き出していってみましょう。

もしもここで『１桁』という条件がついていなければ、ｘはどこまでも書き出していかなければいけないことになり、解は無数に存在してしまうことになりますね。

さて、書き出していった数字をながめながら、あらためて問題を考えてみましょう。

なにか気づくことはないでしょうか？

（１、３）

（２、４）

（３、５）

（４、６）

（５、７）

（６、８）

（７、９）

（８、１０）

（９、１１）

これらの数字のペアをかけあわせた数字が右辺の３ｙということになります。

ｙが自然数ということなので、３ｙは当然『３の倍数』ということになります。

つまり、書き出していった数字をかけあわせて、３の倍数になる場合を調べればいいということです。

ということは、かけあわせる数字のどちらかが、３または３を因数にもつ数字であればいいということですね。

別の言い方をしましょう。

かけあわせる数字のうち片方でもいいので、３の倍数の数字があればいいということです。

そのようなパターンを調べてみると、このようになります。

これらの数字をかけあわせて、出てきた結果を『３×○』というかたちに書き直します。

赤丸をつけた数字がｙの候補になるのですが、『ｙは１桁の自然数』という条件があるので、ｙは１、５、８がその条件にあてはまります。

よって、答えは

（ｘ、ｙ）＝（１、１）,（３、５）,（４、８）

ということになります。

あらためて…灘高校の問題：(1)の解説にもどります。

それでは整数問題のこのパターンの準備運動も終わったところで、いよいよ当初の目標である灘高校の数学に挑戦してみましょう。

ここまでの解説を理解できた方は、この問題は簡単に解くことができるでしょう。

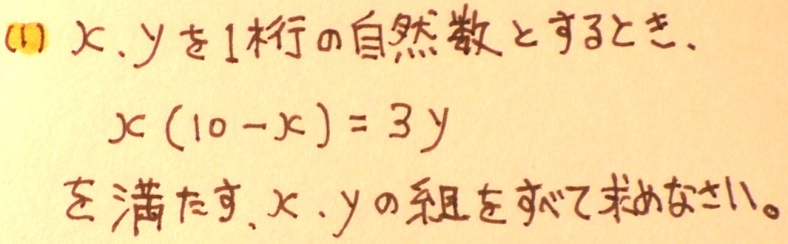題材：灘高校	難易度：★★★☆☆☆☆☆☆☆

この問題はもはや先ほどの解答パターンとまったく同じなので、手短にお話ししますね。

まず、ｘと（１０－ｘ）のペアを書き出していきます。

（１、９）

（２、８）

（３、７）

（４、６）

（５、５）

（６、４）

（７、３）

（８、２）

（９、１）

先ほどの問題と同様、このペアを掛け合わせた数字が３の倍数になればいいということですね。

よって、かけあわせる数字のうち片方でもいいので、３の倍数の数字であればいいので、このようになります。

あらわれたｙの候補はすべて１桁の自然数という条件を満たしていますね。

ということで答えは

（ｘ、ｙ）＝（１、３）,（３、７）,（４、８）,（６、８）,（７、７）,（９、３）

になります。

どうでしょうか。これまでの考え方ですんなり解答できましたね。

さて、次はいよいよ難問の(2)にチャレンジしていきましょう★

灘高校数学：難問の(2)の解説

題材：灘高校	難易度：★★★★★★★★★☆

先ほどの整数問題がどのような誘導になっているか、ここでわかる受験生は非常にすくないでしょう。

が、ともかく問題文から方程式をつくることができますので、とりあえずつくってみましょう。

ただし、各桁の数字ごとに文字をあてがおうとすると、４種類の文字を使わなくてはいけないことになります。

このように、文字が多すぎて収拾がつかなくなります。

なので、ここは『上２桁』『下２桁』をそれぞれX、Yと置き換えて、２種類の文字で式をつくりましょう。

ここで注意するのが『もとの４桁の自然数』の書き表し方ですね。

たとえば１２３４という４桁の数字を、１２と３４という２桁の数字を使って表現しようというとき

１２×１００＋３４というように書き表します。

よってこの場合『もとの４桁の自然数』をX、Yで表現すると

100X＋Y

ということになります。

よって、作られた方程式はこのようになります。

Yの項がふたつあって気持ち悪いので、まとめておきましょう。

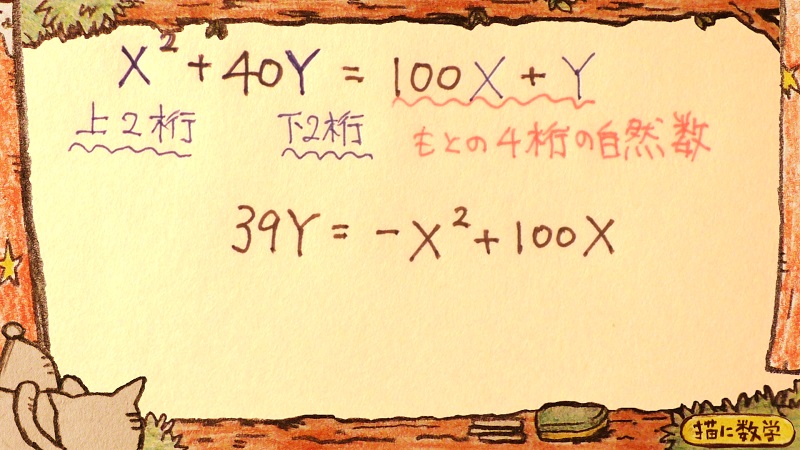
さて、このあとの式変形が重要な岐路になるのですが、２通りの展開が考えられます。

ひとつめは『Y＝Xの式』にする場合です。

実際に変形すると、このようになります。

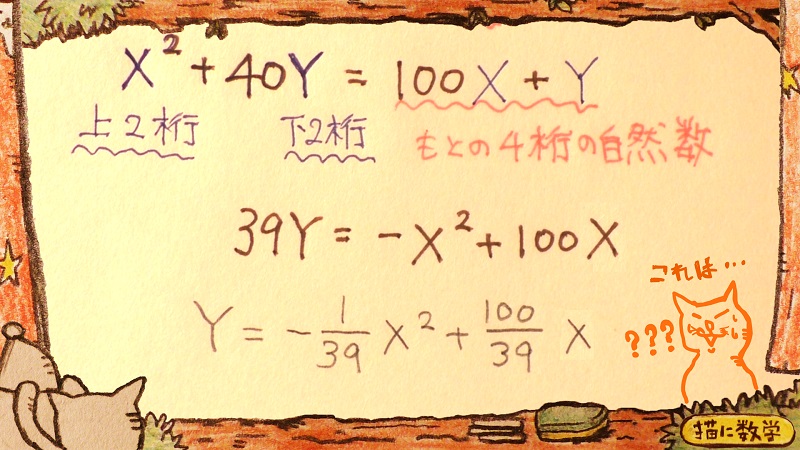
ただ、この変形によって解答をみちびきだそうとするのは至難の業となりますのでやめておきましょう。

なのでここは、(1)の問題が誘導になっているとしたら？という可能性に注意を払ってみましょう。

(1)の問題をながめてみると、この方程式同様、２種類の文字で構成されていることに気が付くと思います。

ということは、(1)の問題と同様の手法でこの方程式から、XとYのペアを見つけ出すことができるのではないか？と考えられます。

(1)の解法が使えそうなかたちに、方程式を変形してみます。

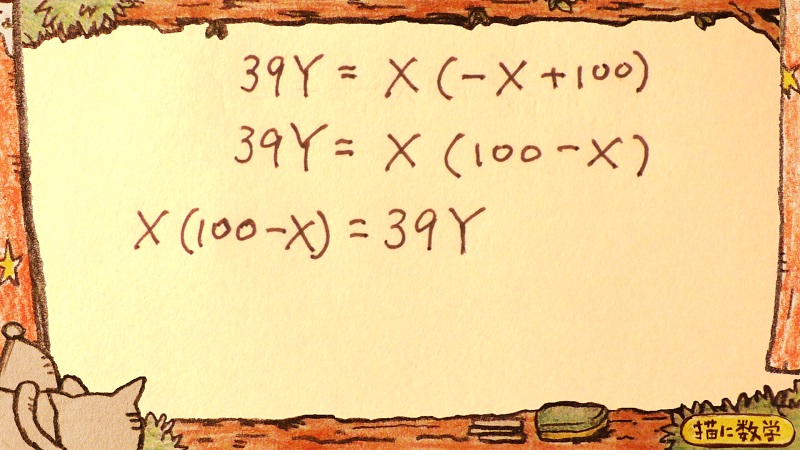
うまく整えられましたね。

ここまで来れば、次にやるべきことは、なんとなく想像できるかと思います。

そうです。

(1)の時と同様、Xの候補を書き並べていくのです。

が、ここで気をつけなければいけないことがあります。

XもYもともに範囲があるということです。

『４桁の自然数』という条件を満たさなければいけないので

『上２桁』の数であるXは『10≦X≦99』

『下２桁』の数であるYは『0≦Y≦99』

という範囲が存在します。

これを範囲を守りながら、Xの候補を書き出していってみましょう。

これをもとに(1)と同様の手法で解こうとして、打ち砕かれた受験生もあろうかと思います。

なぜなら(1)の場合と違って

『Xの候補が多すぎる！！』

ということと

『Yの係数がちょっと複雑！！』

ということに戸惑ってしまうからです。

(1)と同じ考え方でこの出来上がった方程式を眺めた場合、こう考えると思います。

なるほど、Xと(100－X)をかけあわせた数字が39の倍数になっていればいいのか。と

けれども39の倍数というところがちょっとわかりにくいですね。

なぜなら(1)の問題と違い、Yの係数が素数になっていないからです。

この問題の場合だと、Yの係数39は、３と１３という素因数に分解できます。

なので、こういう場合はどうすればいいのか、ということを、もう少しシンプルな例題で説明していきます。

例えば、このような場合だとどうでしょうか。

引用：灘高校：2016年（平成28年）	難易度：★★★★☆☆☆☆☆☆

(1)の問題の右辺を少し変えただけですが、ｙの係数が素数でなくなったため、すこし複雑になっています。

ｘと(10－ｘ)をかけあわせた数字が６の倍数になっていればいい、というとらえ方の発想は今まで通りですが、

かけあわせると６になるためには、Xと(10－X)がどうなっていればいいのか、ということを考えます。

６は２と３という素因数に分解されます。

なので、ｘと(10－ｘ)のどちらかの因数に、２と３が入っていればいい、ということになります。

２の因数を持つ数字は２の倍数であり

３の因数を持つ数字は３の倍数なのですから

２の倍数、３の倍数をそれぞれチェックしていきます。

赤丸も青丸も両方チェックが入った（ｘ、10－ｘ）の組み合わせが、

『かけて６の倍数になる』という条件をみたしたものですから

それらを『６×○』という表現になおします。

これらのｙの候補はすべて『１桁の自然数』という条件を満たしますから

（ｘ、ｙ）＝（４、４）,（６、４）が求める答えとなります。

このようにして(2)も対応していくのですが、(2)はそもそも書き出してゆくXの候補が多く、手間がかかるように思ってしまいます。

ですが、この問題に限って、それを少し簡略化することが実は可能なのです。

どういうことかと言うと、いまのこの問題をもういちど見てください。

これは、（ｘ、10－ｘ）の候補となる数字の組み合わせについて、縦に書いていったものです。

書き出していった候補の真ん中（５、５）に注目してください。

このペアを境に（ｘ、10－ｘ）の候補は、それまで書き出していった数字を互いに入れ替えたような現れ方になっていますよね。

するとかけ合わせた数字だけを見ると、やはり『互いに入れ替えた』だけのペアの場合と同じ結果に、当然なります。

たとえば（３、７）というペアを互いに入れ替えた（７、３）というペアは、どちらも『かけて２１』という結果になるわけです。

かなり当たり前のことを話しているようですけれど、これを利用することで、この(2)の問題は話がグッと楽になります。

ほんまにやっとこさ(2)の解説に入れるわ…

話を(2)に戻します。

まず、この話を理解しやすいように『10≦X≦99』という条件を少し変更します。

Xの範囲を『1≦X≦99』として説明を進めますね。（もちろん後でなおします★）

（X、100－X）の候補を1から99まで書き出していくと、このようになります。

Xと(100－X)をかけあわせた数字が39の倍数になるためには

Xまたは(100－X)のどちらかの因数に、3と13が入っていればいい、ということになります。

ここで、仮に、さっきと同じ要領で、

３の因数を持つ数字は３の倍数であり １３の因数を持つ数字は１３の倍数なのですから ３の倍数、１３の倍数をそれぞれチェックしていきます。

…というようなことをしようものなら、どえらい手間がかかってしまいます。

けれどもさっき言ったように、この場合は（５０、５０）のペアを境に、

これまでとおなじ数字のペアが、互いに入れ替わってあらわれてきます。

さらに、３の倍数はかなりの候補が存在しますが、１３の倍数はそんなに多くはありません。

１から９９までの数字で、１３の倍数は

１３、２６、３９、５２、６５、７８、９１、の計７つです。

Xの候補にも、(100－X)の候補にも、１３の倍数はそれだけあらわれます。

Xまたは(100－X)のどちらかの因数に、3と13が入っていればいいということですが

逆に言えば、Xにも(100－X)にも１３の倍数が入っていないようなペアは、はなから除外、ということになります。

ということは、Xの候補のなかの１３の倍数である７つの数字に対応する(100－X)が、３の倍数になっているかどうかを調べればいいということになります。

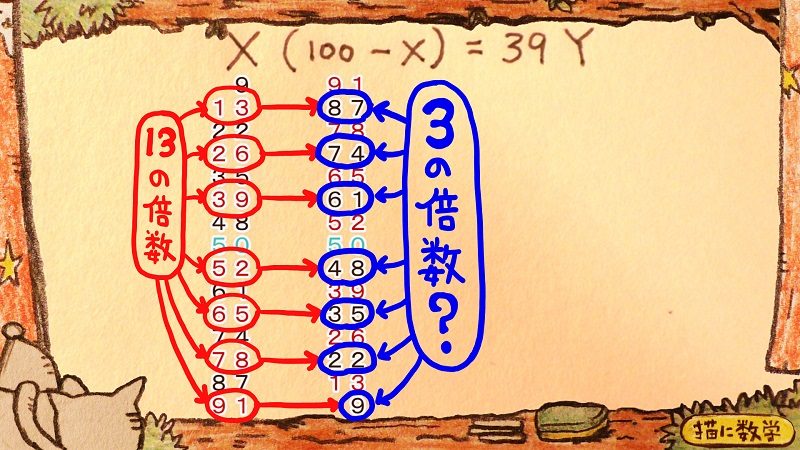
ただし、３９、７８、という数字は３９の倍数ですので、調べるまでもなく、すでにその数字だけで因数を３と１３の両方をもっています。

なので、正確にはその２つを除外した、残りの５つについて検証していくだけとなります。

今の話は

『Xの候補のなかの１３の倍数だけ、そのペアとなる(100－X)の数字がはたして３の倍数になっているのかどうかを調べよう』

という話でした。

もしかしたらここで

『(100－X)に書き出していった１３の倍数の数字に対応するXが、３の倍数になっているのかどうかを調べる必要はあるのか？』

と思う方がいるかもしれません。

けれども、その手間は必要ありません。

なぜなら、さっき話したように、求めたい数字のペアさえ見つかれば、あとはそれを互いに入れ替えたペアもまた、『かけて３６の倍数になる』という同じ結果になるからです。
１３の倍数は

１３、２６、３９、５２、６５、７８、９１、でした。

検証すべき（X、100－X）の候補を書き出すと

（１３、８７）

（２６、７４）

（５２、４８）

（６５、３５）

（９１、９）

になります。

３９、７８、は３９の倍数なので

（３９、６１）

（７８、２２）

は、(100－X)を調べなくても、かけて３６の倍数になるということがわかります。

３の倍数であるかどうか、ということを調べるには、各桁の数字をたした数字が３の倍数になるかどうか、をチェックすればいいのでしたね。

たとえば８７という数字は、各桁の数字である８と７をたして１５になります。

１５という数字は３の倍数ですから、８７も３の倍数ということになります。

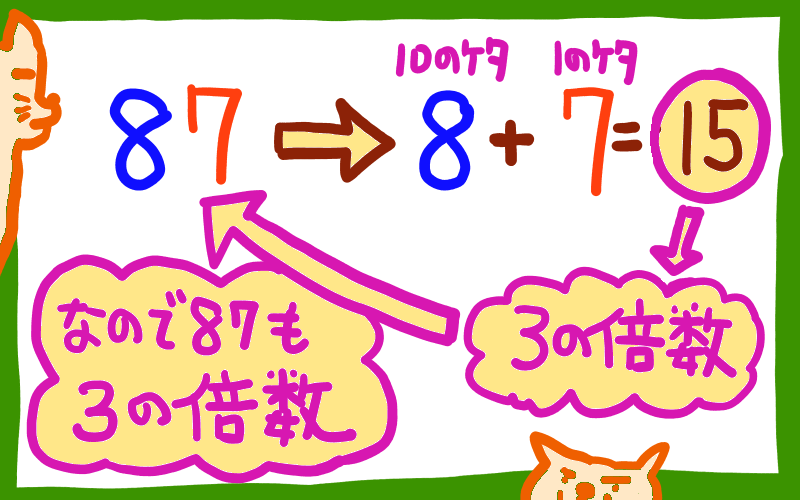
こうやって調べていくと、４８と９も、３の倍数だということがわかります。

（１３、８７）

（２６、７４）

（５２、４８）

（６５、３５）

（９１、９）

と、このようになりました。

結局、（X、100－X）の候補として生き残ったのが

（１３、８７）

（３９、６１）

（５２、４８）

（７８、２２）

（９１、９）

これはつまり、Xが１３の倍数のとき、という観点で調べた結果です。

さらに先ほどこのようなことを言いましたね。

求めたい数字のペアさえ見つかれば、あとはそれを互いに入れ替えたペアもまた、『かけて３６の倍数になる』という条件を満たす

つまり、Xと(100－X)の候補を互いに入れ替えた数字のペアもまた、かけて３６の倍数となる候補になります。

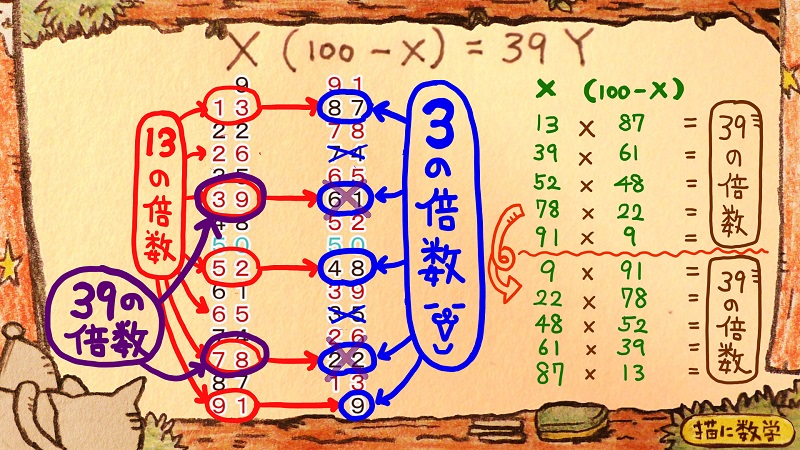
これですね。

（８７、１３）

（６１、３９）

（４８、５２）

（２２、７８）

（９、９１）

こっちは、(100－X)が１３の倍数のとき、という観点で調べた結果とも言えます。

ここで、本来の問題にあった『10≦X≦99』という条件を適応させると

（９、９１）

が除外されることになります。

生き残った９通りのXに対し、対応するYを求めます。

（X、Y）＝（13、29）,（39、61）,（52、64）,（78、44）,（91、21）,（87、29）,（61、61）,（48、64）,（22、44）

となり、求める４ケタの自然数は、上記のようになりましたね。

灘高校入試突破の思考力を体験していただけましたか？

今回も説明が長くなってしまってすみません。

どのようなレベルの方でも、できるだけわかりやすいように説明しようとするあまり、かなり言い回しがくどくなりすぎているかもしれません。

この『猫に数学』では、難関高校を受験しようという子に対して、特に独学では理解しにくそうな問題をピックアップして解説をしています。

紙面の限られた過去問題の解説などを読んでも、解答へといたる発想や論理的な思考の流れまでは、なかなかとらえにくいものです。

この講座が少しでも、数学の勉強のお役にたてたとしたら、僕も幸いです。