開成高校の数学過去問をわかりやすく解説。

題材：開成高校、國學院大學久我山高校	難易度：★★★★★☆☆☆☆☆

どうも、サカタです☆

この講座『猫に数学』では、おもにハイレベルな中学数学をメインに解説していきます★

高校入試の数学を独学していこうという中学生のためのお助けページとなれば幸いです。

今回は、高校入試数学でよく使われる手法

『連立方程式』についての難問パターンをとりあげ解説していきます。

また、具体的な入試対策用として、開成高校、國學院大學久我山高校の数学入試問題の過去問を引用しつつ、話を進めていきますね。

今回の扱うテーマであり、目標とするレベルの問題はこれです。

目標レベル：開成高校の数学（2016年の過去問）

引用：開成高校：2016年（平成28年）	難易度：★★★★★☆☆☆☆☆

これが今回、目標とするレベルの問題ですが、この難問の解説をしていく前に、いろいろと話さないといけないことがあります。

特に、連立方程式の解がないとはどういうことか？

ということを説明していく前に、連立方程式の解ってなに？

ということも話していこうと思います。

連立方程式の解がないってどういうこと？

連立方程式の解について、あなたはきちんと理解していますか？

このことについて問題にしてくる高校入試問題が、主に難関校で見られます。

なので、まずは、連立方程式の基本から説明していきます。

え？　連立方程式の解が存在しないってどういうこと？

そもそも連立方程式の解ってどういう意味？

連立方程式ってなんやったっけ？

などなど、いろいろな疑問が浮上してくると思います。

一応、教科書レベルの範囲外かつ、高校数学で扱うテーマではあるのですが、

連立方程式の本質を理解すれば、そのまま入試問題で対応できる話になっています。

なので、できるだけ難しい言い回しは省いて説明していきます。

最終的な目標レベルとしては、難関校、開成高校の数学過去問を解けるようになりましょう。

そもそも連立方程式って何やったっけ？

最初に考えなければいけないのは、連立方程式の解とは、つまりなんなのか？ということです。

この開成高校の過去問には、『連立方程式に解がないとき』という前提がありますが、

そもそも連立方程式の「解がある」「解がない」とはどういうことなのでしょうか？

中学数学で習う範囲においては、ほとんどすべてが「解がある」という前提で問題がつくられています。

なので、そもそも「この連立方程式には解があるのかないのか」などということは多くの中学生は考えたりもしません。

ここで、連立方程式についての基本的な理解を確認していきましょう。

この問題を見てください。

これは僕が家庭教師で、小学生に足し算の計算を指導する際、よく解かせていた問題です。（現在は小学生の指導はしていませんが。）

この場合、答えは複数ありますし、答えを整数に限定しなければ、無限に解答していくことができます。（例：3.4＋6.6＝10　などなど）

また、これに慣れてきたら、このような問題も出題していきました。

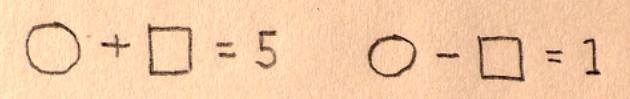
同じ記号には、同じ数字がそれぞれ入る、という条件がこの問題にはあります。

なので、両方の式が等式として成り立つように数字を入れていかなければなりません。

この程度の問題だったら勘を働かせて、正解を探し出すことも可能でしょう。

または、しらみつぶしに探すとなった場合、答えの候補を書き出していくということをするでしょう。

たとえばこのように。

この書き出した候補のなかから、互いに共通する数字のセット（□と○のセット）を探し出せればそれが正解、ということになります。

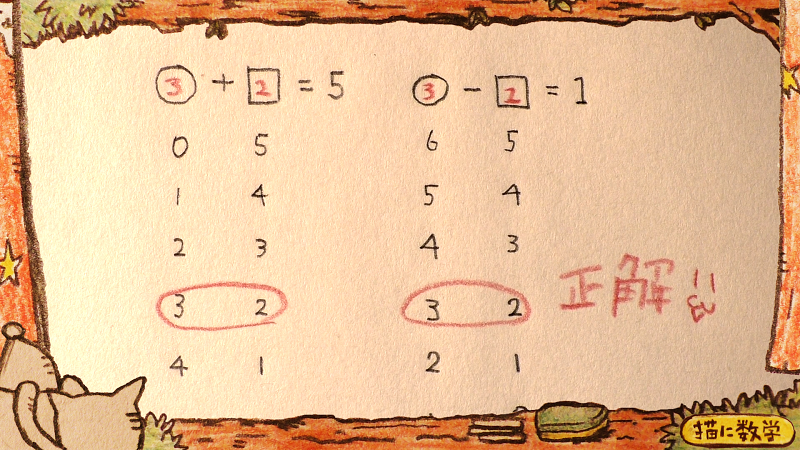
実はこれが『連立方程式を解く』ということの本質になります。

さっきの問題を○をｘ（エックス）に、□をｙ（ワイ）に書き換えてみましょう。

こうなります。

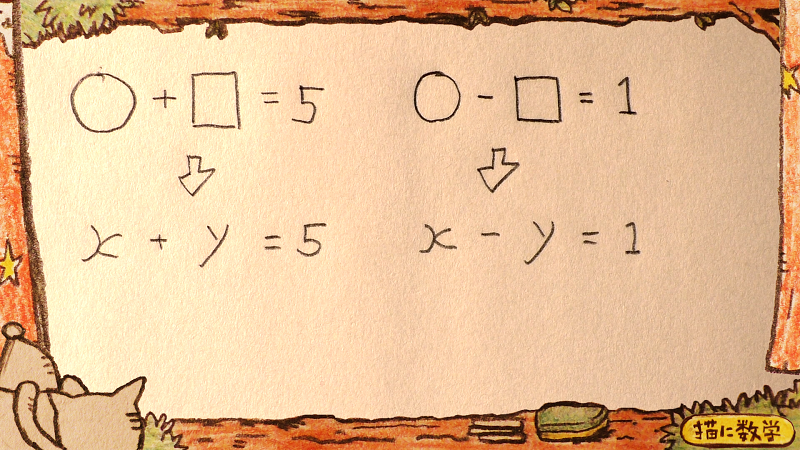
これをそのまま加減法で解いてみましょう。

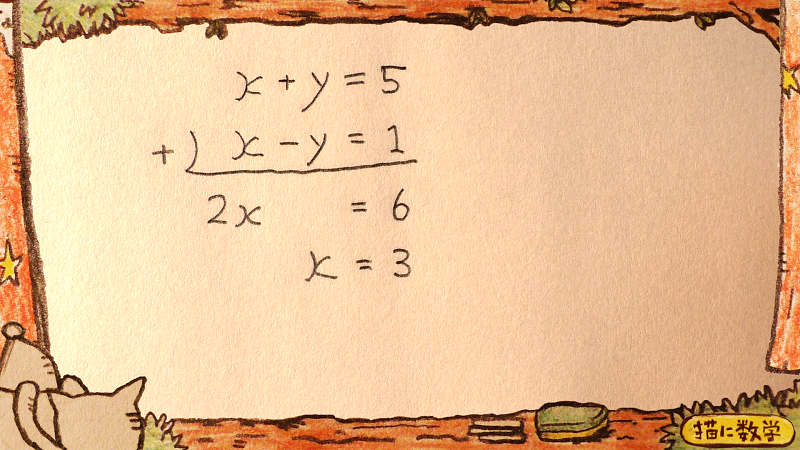
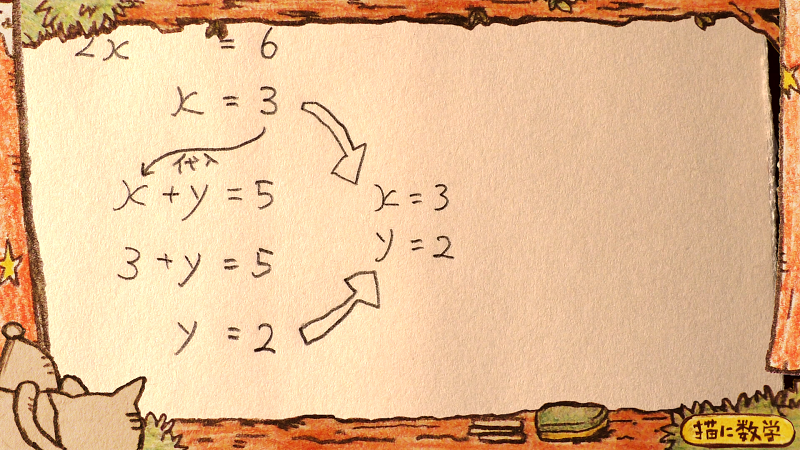
どうでしょうか？

さっさの答えと同じになりましたね。

※少々、記述方法が我流すぎますが、実際の解答用紙には、こんな書き方をしないでくださいね。展開の流れをわかりやすくするために使った、ここだけの書き方です。動画を見てもらうと、計算の流れがもっとわかりやすくなっています。

連立方程式の本質について。グラフという観点から理解しよう☆

それではここで、この二つの数式を、関数としてグラフに書いてみます。

するとこうなりますね。

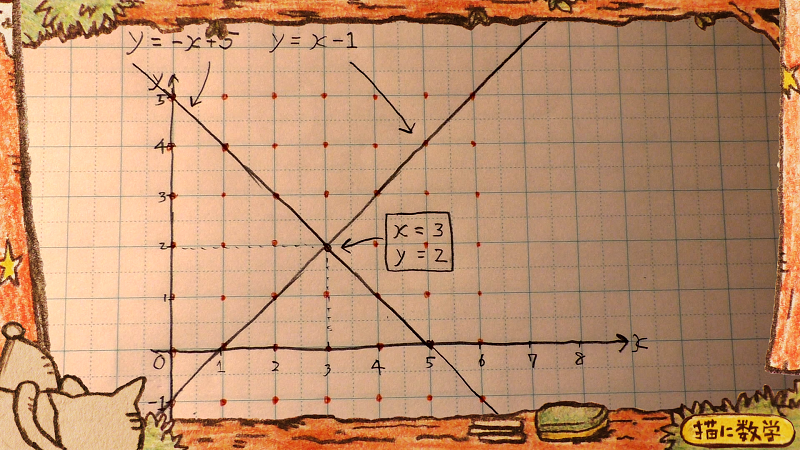
さて、ここで何か気づくことはないでしょうか？

さっきの画像と合わせて見るとこんな感じになります。

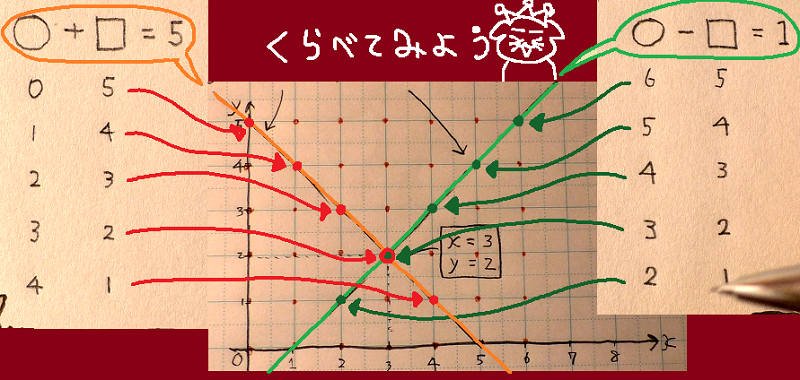
これをみるとわかるように、関数の各座標が整数になるポイント(難しく言うと、それを格子点といいます)が、ちょうど先ほど「書き出していった答えの候補」と一致するのです。

そして、この直線上にある座標のｘとｙのセットであれば、両方とも整数でなくても（格子点上でなくても）その関数の等式を成り立たせるｘとｙのセットであるということも理解できます。

たとえばこの点のｘとｙのセットは、そのグラフの等式を成り立たせますよね。

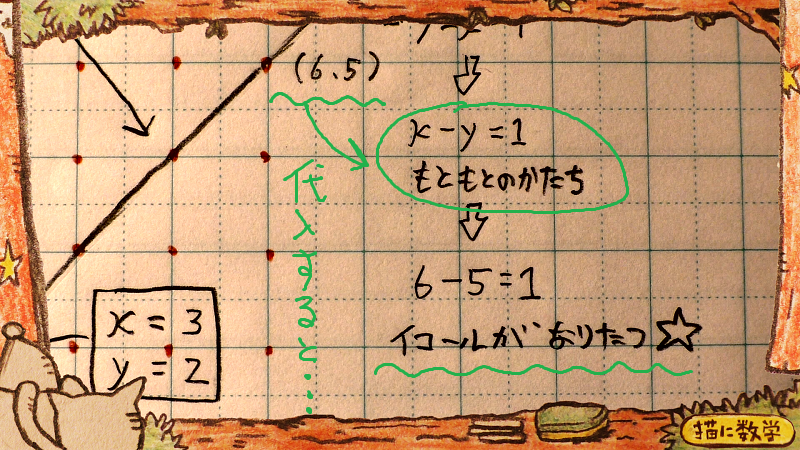
整数以外もちょっと試してみます。

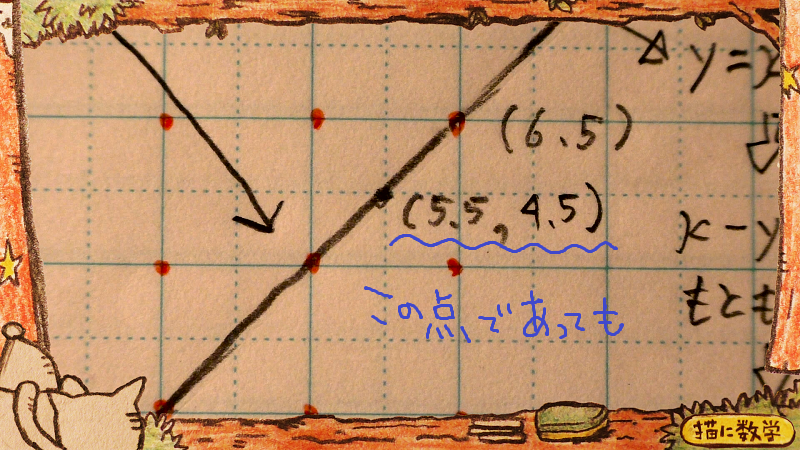
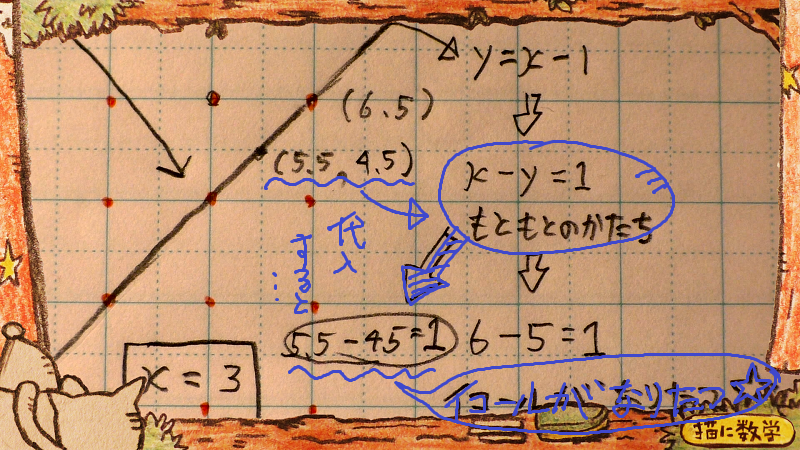
やはり、イコール関係が成り立ちましたね。

ここでちょっとこの関数から外れた点の数字（ｘとｙのセット）を代入してみましょう。

こんなふうに、イコールが成り立たず、等式が成り立ちません。

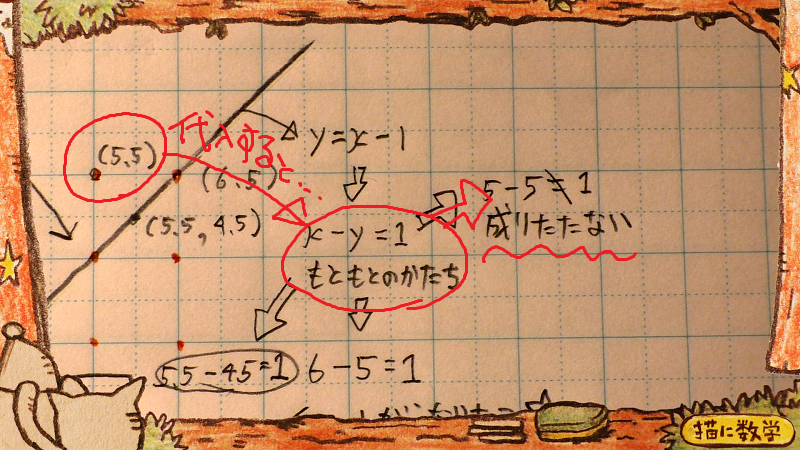
つまり、ｘとｙの関数をグラフ化した場合、その線上の座標（ｘとｙのセット）であれば、どこを代入しても、その関数の等式を満たす、ということですね。

なんだかすごく当たり前の話に聞こえる方もいるでしょうが、もうちょっと我慢してください。

そして、この場合、二本のグラフの交点が、連立方程式の解になっていますね。

ここから、このようなグラフの見方をすることができるということがわかります。

交点の座標	両方の関数の等式を成り立たせる
交点以外のグラフ上の座標	片方の関数の等式を成り立たせる
グラフ上にない座標	両方の関数の等式を成り立たせない

つまり、『連立方程式を解く』ということは、グラフ上に置き換えてみれば『その交点の座標を求める』ということにほかなりません。

別の言い方をすれば、『連立方程式が解ける』ということは、グラフ上に置き換えてみたときに『その交点が存在する』ということでもあります。

じゃあ、連立方程式が解けない場合、そのグラフはどんな様子になっているのでしょうか？

それでは、いよいよ核心に入っていきましょう。

連立方程式の解がない条件とは？

それでは、次の問題で『連立方程式の解のない条件』について、いよいよ本質に迫っていきましょう。

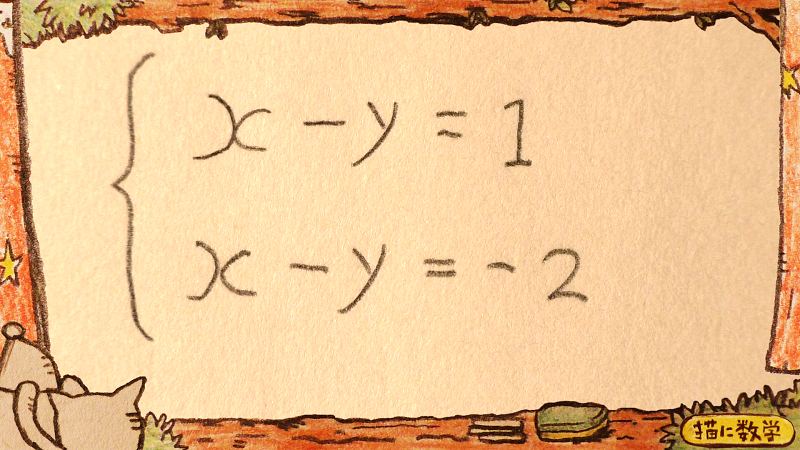
さて、この問題は、どうやったって解けません。

加減法で解こうが、代入法で解こうが、ｘとｙがともに消えてしまって、残った数式自体も、左辺と右辺のイコール関係が成り立ちません。

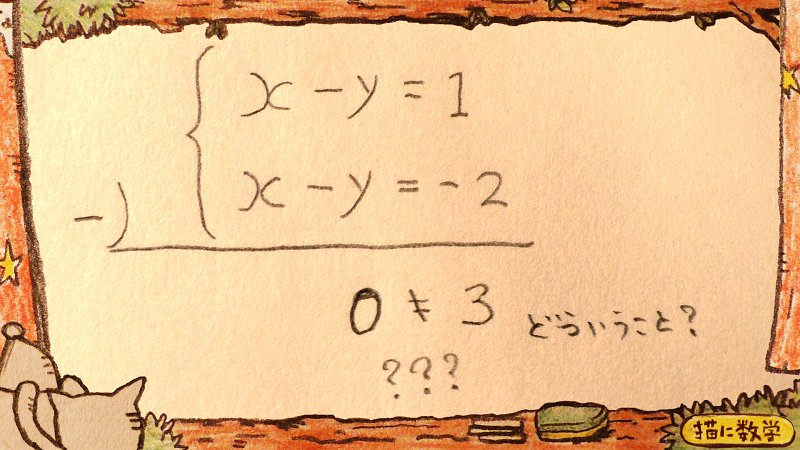
これはいったいどう解釈すればいいのでしょうか。

グラフに置き換えて考えてみます。

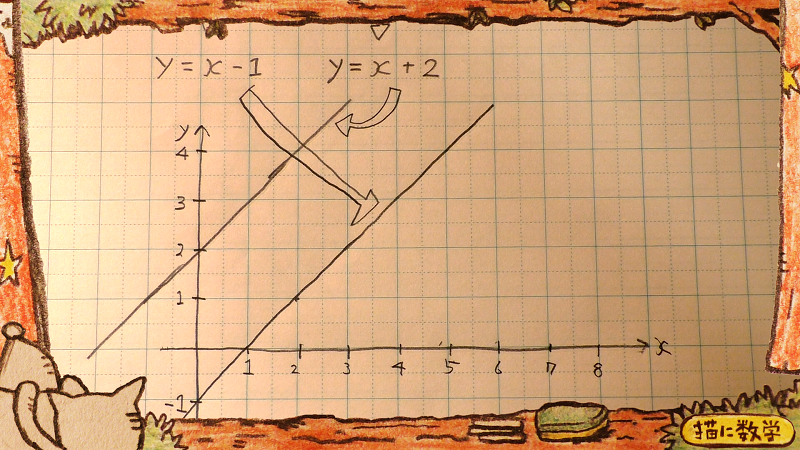
これは、さっきの関数を変形し、グラフ化したものです。

ご覧のように、二本の直線は互いに平行なため、その交点が存在しません。

つまり、『２つの関数の等式を成り立たせるような、共通したｘとｙのセットが存在しない』ということであり

『この連立方程式には解が存在しない』ということを指し示しているのです。

これは、グラフを書いてからわかったことです。

では、この連立方程式に対して、グラフを書かないで、解が存在するかどうかを確かめようとした場合は、いったいどこをチェックすればわかるというのでしょうか。

グラフを書いてからだと、交点がないということがわかったので、明らかに『解なし』と判別できました。

ということは、この二本の直線が平行である条件、つまり、『傾きが同じであるのかどうか』ということについて調べてみればいいことになります。

例えばこのような問題の場合を見てみましょう。

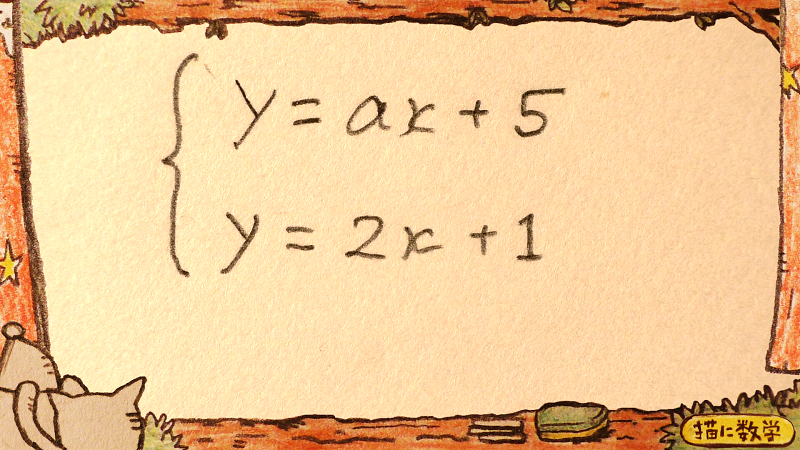
この連立方程式に解が存在しないということは、その傾きが互いに等しいということですから、このようになります。

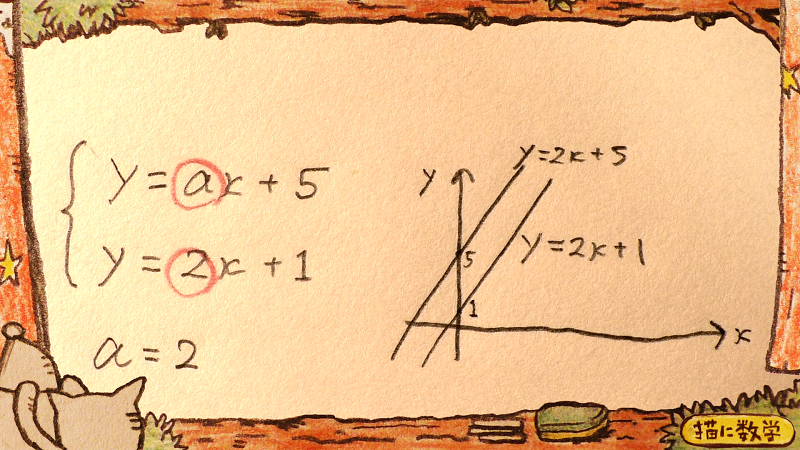
このように、傾きを比較したところ、定数aが２であればいい、ということになります。

基本的に、このような問題の場合は、交点と傾きを意識したアプローチで攻略できます。

それでは次は実践レベルでの解説を交えていきましょう。

國學院大學久我山高校の数学（2016年の過去問）

引用：國學院大學久我山高校：2016年（平成28年）	難易度：★★★☆☆☆☆☆☆☆

どうでしょうか？

これまでの知識をもってすれば、解答できたのではないでしょうか。

解法のポイントは、まずは傾きを比較できるように式変形することです。

出題された問題のままでは比較できないので、まずは式変形をしましょう。

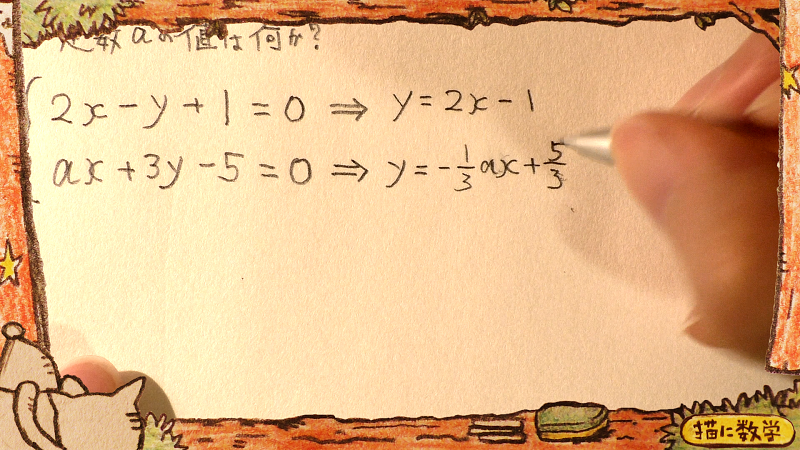
すると、このようになります。

この時点でグラフはこのようになります。

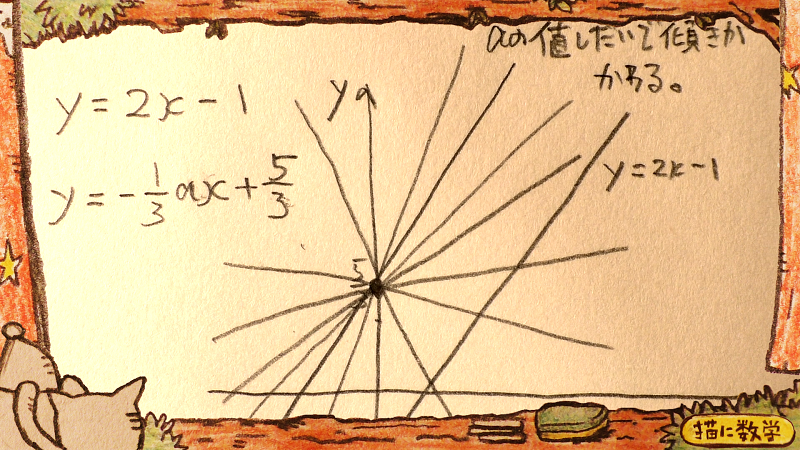
つまり、ここで二つの式の傾きが同じになるようなaの値を求めればいいということになります。

ご覧の通り、これでaが求まりました☆

ハイレベル数学の入試対策～この問題のよくある落とし穴

一応この類の問題を解くための基本的な概念についてざっと説明しおわりましたが、さてここで、疑問に思った方もいるのではないでしょうか？

もしもグラフ上の２本の直線が完全に一致した場合、連立方程式の解はどういうことになるのだろうか？と。

これがこの問題でうっかりミスをしてしまうポイントのひとつであり、気を付けなければならないところです。

たとえばこのような問題の場合、あなただったらどう考えるでしょうか。

引用：オリジナル問題	難易度：★★★☆☆☆☆☆☆☆

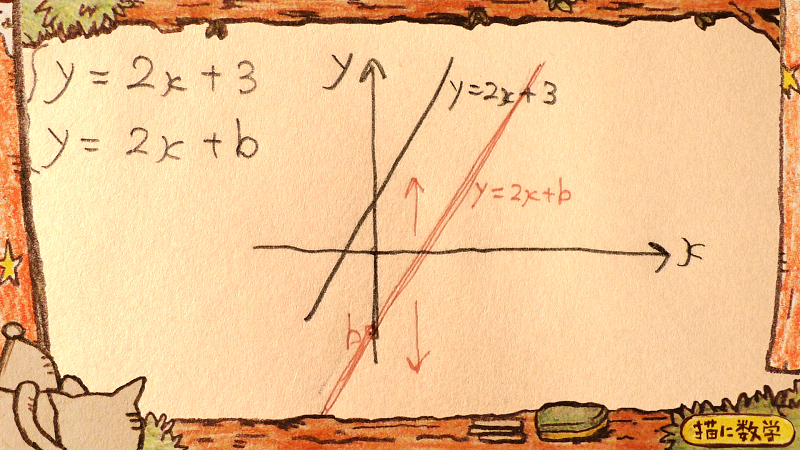
この場合、グラフで置き換えてみればわかるように、bはどんな値をとってみても交点は現れないように思われます。

けれどもちょっと考えてみてください。

もしもｂが３なら、２本の直線は完全に一致します。

その時、連立方程式の解はどういった結果を指し示すのでしょうか。

ちょっとここで、実際に解いて確かめてみましょう。

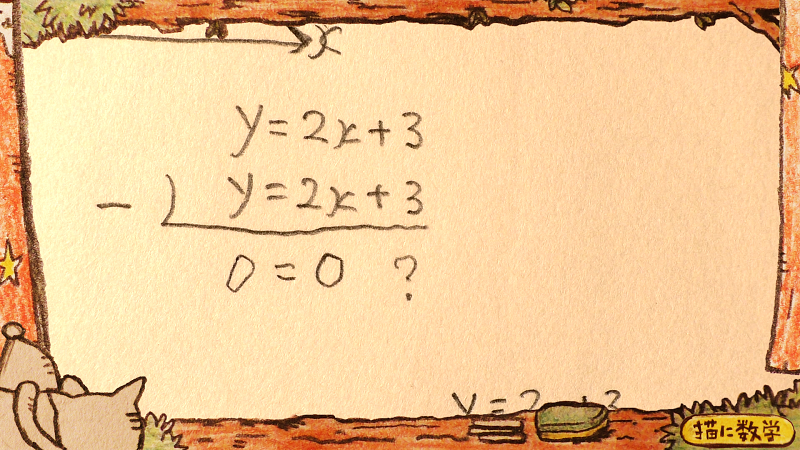
加減法で解こうとも、代入法で解こうとも、ｘとｙがともに消えてしまいます。

ということは、これも『解なし』なのか？と思ってしまうかもしれませんが、ちょっと待ってください。

この説明の少し前に、『解がない』という結果がでる場合の問題を扱いましたね。

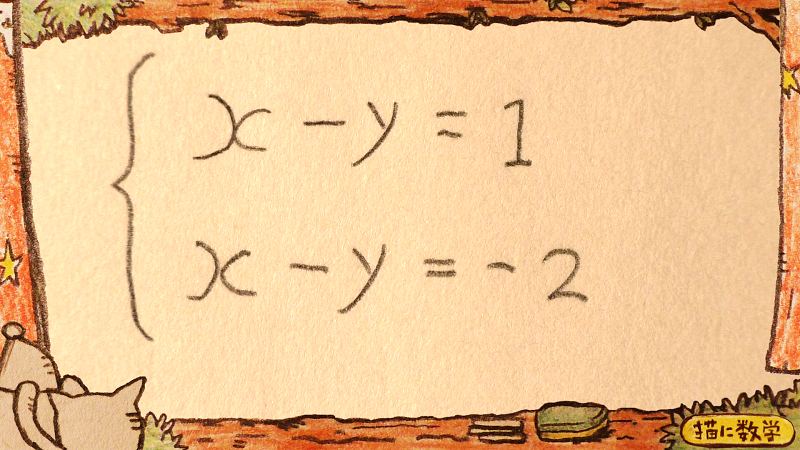
この問題を加減法で解くと、こういうことになります。

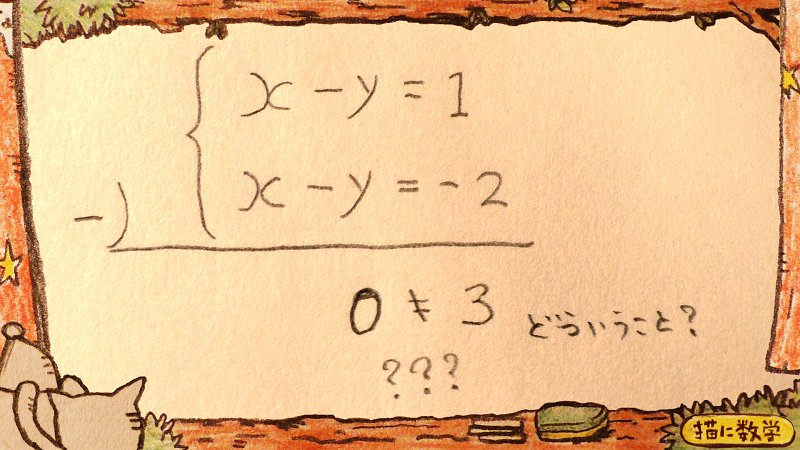
ｘとｙがともに消えて、なおかつ残った方程式自体にもイコールが成り立たないですね。

これは、どういうことなのか？

ちょっとわかりにくいかもしれませんが、消えてしまったｘとｙをそれぞれ「０かけるｘ」「０かけるｙ」というように置き換えて考えてみると理解しやすいです。

と、この場合、ｘとｙにどんな数字を入れても、左辺と右辺のイコール関係が成り立ちません。

これが『連立方程式の解がないときの特徴』です。

かたや、今回の問題の場合、ｘとｙにどんな数字を入れても、左辺と右辺のイコール関係が成り立ってしまいます。

どういうことかと言うと、これもまた、消えてしまったｘとｙをそれぞれ「０かけるｘ」「０かけるｙ」というように置き換えてみればわかりやすいです。

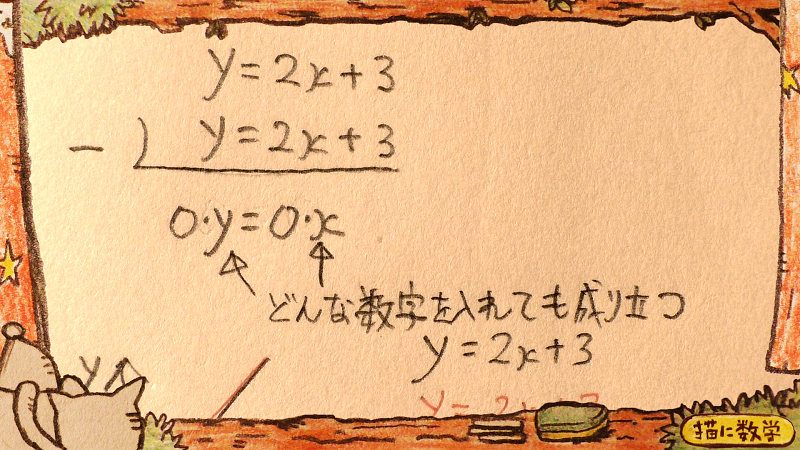
２式が完全に一致する連立方程式においては、最終的には、０・ｘ＝０・ｙという等式になり、ここのｘとｙにどんな数字を入れようとも、０イコール０という結果として、等式がなりたってしまいます。

つまり、この２つの関数のｘとｙに、どんな数字を代入しようとも、等式が成立してしまうということです。

ただし、加減法で扱ったもともとの式の条件も満たさないといけないので、解はどんな数字でもいいわけではありません。

もともとの連立方程式に登場した関数の式の条件も満たさないといけないので、結局は、その関数の直線上の座標であればどんなｘとｙのペアでも解として認められるということになります。

ここもまた、わかりにくいところかもしれません。

以下、これまでの話を表にしてまとめてみました★

一次方程式の連立方程式の解の現れ方には、３種類あります。

解が一組ある。 解が無数にある。 解がない。

傾きが異なる場合は、解が一組現れます。

傾きが同じであった場合、確かに『解がない』ということになるのですが、その関数が完全に一致した時に限り、『無数に解がある』ということになります。

この問題のように、２つの関数の傾きが最初から同じであった場合、交点が存在しないか、完全にグラフが一致するかのどちらかしかありません。

完全に重なった場合、２式の直線上のすべてが、ともに等式を満たすｘとｙのセットとして、連立方程式の解になります。

なのでこの問題の場合、連立方程式の解を存在させないためには、２本のグラフを互いに平行の位置関係にしつつも、完全に一致させてはいけないということになります。

よって『ｂは３以外のすべての実数』ということになるのです。

開成高校の数学難問にチャレンジ

それではいよいよ高校入試数学の最高レベルに挑戦してみましょう。

この内容は高校数学の知識があれば教科書レベルで解くことが可能なので、難易度の★マークはあえて５つにしています。

引用：開成高校：2016年（平成28年）	難易度：★★★★★☆☆☆☆☆

まずこの問題を見て『なんか式が複雑やなあ』とひるんだ方もいると思いますが、とりあえず傾きとｙ切片が比較できるよう、式変形をしましょう。

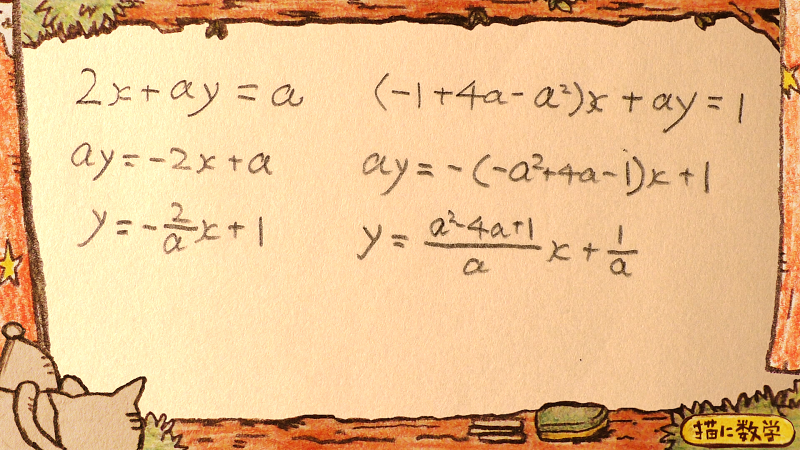
さて、ここで考えなければならないことがあります。

この形にもってくるまえに、疑問もしくは違和感を感じた方がいるのではないでしょうか。

そうです、分母に文字がきています。

『分母にゼロがきてはいけない』というのは、数式を扱う際の大前提です。

分母に文字や文字式がきている場合、それがゼロではないという確認をとるか、それがゼロでないという場合として話を進めていかなければなりません。

この場合、傾きにもｙ切片にも分母にaが入っていますが、ここから先の話はaがゼロでないという前提で話を進めていかなければなりません。

というより、式変形の前の段階で、「a≠0の場合」として記述していかなければいけません。

つまり、計算の結果、最終的にaイコール０になったとしても、それは答えの候補からはずさなくてはならないということです。

このことを踏まえて、さらに問題を解き進めていきましょう。

連立方程式の解が存在しないための条件は、互いのグラフの「傾きが同じ」かつ「ｙ切片が異なる」でしたね。

つまりこういうことです。

≠（ノットイコール）があることで戸惑った方もいるでしょうが、方程式を解く要領でそのまま解いていけます。

方程式を解く手順はそもそも、論理的な展開を数字と記号で説明していく書き方になっています。

授業動画では省略していた部分なので、ここで具体的に説明しましょう。 このような問題があったとします。 問題：ある数に３を加えると６になった。ある数を求めよ。 ある数に３を足したもの＝６ ということが言えるのですから その両辺に３を引いてもイコール関係は保たれます。 ある数に３を足したもの引く３＝６引く３ ある数＝６引く３ つまり、ある数＝３ ということになります。 このようにして、方程式は論理的に展開されていくのですが、 この話における＝を≠に置き換えても、その論理的展開に支障はありません。 ちょっとためしてみましょう。 問題：ある数に３を加えると６にならなかった。ある数は少なくともどんな数字でないか求めよ。 これをさっきと同じ書き方で表すとこうなります。 ある数に３を加えたもの≠６ この式の両辺にそれぞれ３を引くと、もともと同じでなかった両辺は、あいかわらず『同じでない』という関係が保たれます。 よって ある数に３を足したもの引く３≠６引く３ となります。 よって ある数≠６引く３ となり、 ある数≠３ となります。 確かにある数が３の場合に限り、等式が成り立ってしまいますし、それ以外の実数の場合は、どれも等式が成り立ちません。

このように、≠の場合も、これまでの方程式と同じ要領で解いてゆくことができるのです。

この開成の問題もその手法を使います。

最終的に、求めたaはこのようなことになります。

a≠0の場合
傾きが同じという条件によるaの値	a＝１または３
y切片が異なるという条件によるaの値	a≠１

a≠０の場合として話を進めていますので、aの候補として0が出てきた場合はそれは除外しなくてはなりません、が、今回は出てきませんでしたね。

傾きの条件による計算からは、a＝１または３というように、aの候補が２つ出てきたのですが、

y切片の条件による計算から、a≠１という結果が出ましたので、a＝１は除外します。

「aは１または３であり」なおかつ「aは１ではない」という読み取り方をするのです。

つまり、a＝３がこの場合の答えになります。

もしもこれが、a≠１ではなく、a≠５などという結果だった場合、１も３も答えとして採用ということになります。

その場合、「aは１または３であり」なおかつ「aは５ではない」という読み取り方になります。

とりあえずここまでは理解できたでしょうか？

わからないところがあったら、お問合せフォームなどから質問していただければ、補足説明を加えていきますね★

さすが開成の数学…最後の落とし穴「a＝0の場合分け」を攻略しよう☆

と、ここまで解いて答え合わせをした方はビックリしたと思いますが、実はこれではまだ詰めが足りていません。

このa＝３はa≠０の場合を前提として導き出された答えでした。

では、a＝0の場合はどうでしょうか。

このような問題の場合、a≠0の場合だけ確認して、a＝0の場合は確認しない、という検証の仕方はあり得ません。

ということで、実際にaに数値0を代入して、式の様子を確認してみましょう。

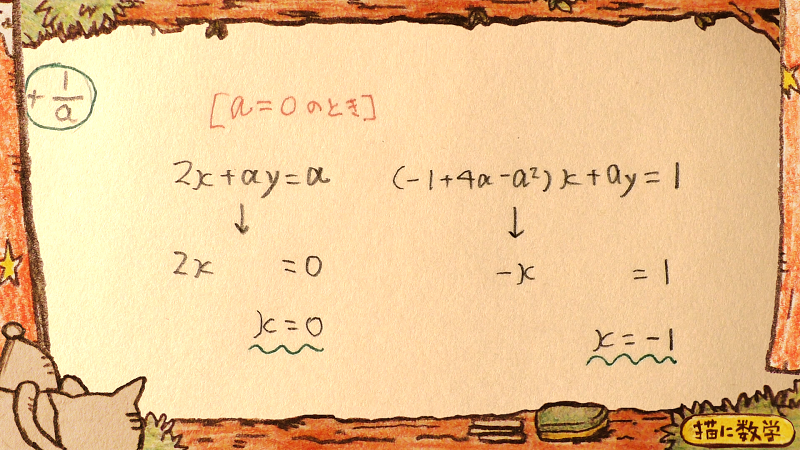
ｘ＝0
ｘ＝-1

という2つの式ができました。

ん？これってどういうこと？と思われるかもしれませんが、迷ったときはとりあえずグラフを書いて事態を確認してみましょう。

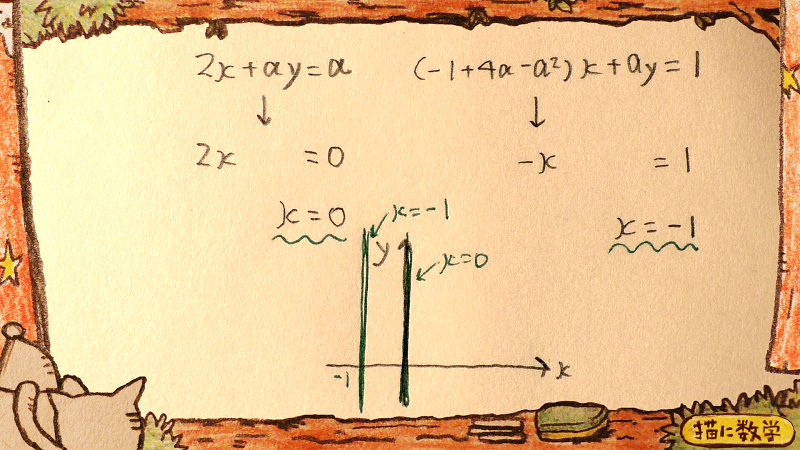
特殊な形なので、戸惑ってしまいそうですが、本質はこれまでと同じです。

この二本のグラフに解があるかどうかは、交点があるかどうかをチェックすればいいということでしたね。

このグラフに交点はなさそうですね。つまり、これも連立方程式の解がない場合として認められるということです。

つまりこの場合のaの数字である０も、答えとして採用されることになります。

よって答えはa＝０、３ということになります。

ふう。お疲れさまでした。

開成の数学だけあって、なかなか手間のかかる問題ですが、高校入試以降も必須の概念です。

大学入試で数学をバリバリ使うつもりの中学生は、これを機会に、理解を深めておくといいでしょう。

それでは、また次回お会いしましょう★

※今回のように、毎回、難問を取り上げ解説していきますが、この講座は主に、解答へとたどり着く思考の手順に重きをおいて説明しています。

なので『解答欄に記入する正確な記述例』をきちんと知りたいという方は、過去問題集の解答を参考にするか、お近くの頼れる先生方に直接聞いてくださいね☆