わかり易いアニメで解説☆一次不等式の解き方~超基本問題

こんにちは、坂田です☆
今回は、一次不等式の解き方の手順を解説します。
一次不等式とか、二次不等式とか、なんのこっちゃと思っている方もいるかもしれませんね。
二次、というのは2乗まで登場する、ということです。
なので、今回は、2乗とかは登場しない、普通の不等式だと思ってください。
まずは、ご覧いただいているこの不等式から説明していきます。
ちなみに等式というのは=で両辺が結ばれた方程式のことを言います。
等式の等は、『等しい』つまり同じという意味ですね。
1+4=2+3
は左辺も右辺も同じ値になりますよね。
今回はそれに否定の意味である『不』が付いた『不等式』を解説します。
つまり、左辺と右辺は同じではないよ、という式なんだな、ととりあえず思ってもらえるとわかりやすいです。
それでは説明していきます。
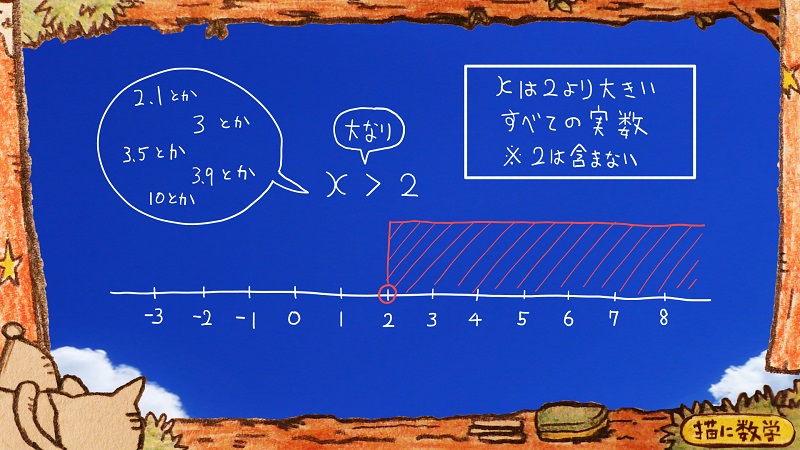
まず、この真ん中に書かれている不等式は
えっくす大なり2
と読みます。
xのほうに大きく口が開いていますね。
なので、
xと2とを比べたらxのほうが大きいよ
と言っているのだと思ってください。
2よりも大きい数字と言えば
例えば、
2.1とか
3とか
3.5とか
3.9とか
10とか
まあ
いろいろありますよね。
それを
数直線上に表したのが
赤いゾーンになります。
2よりも大きい数字のところがすべて赤色になっていますね。
ただ、ちょうど2のところをギリギリ塗ることはできません。
なぜならxは2よりも大きい数字、ということなので
2は含むことはできないからです。
なので、2のところの〇は塗りつぶしていませんね。
また、このxの範囲について難しい言い方をすると
『xは2よりも大きいすべての実数』
という言い方ができます。
たしかにxは2よりも大きいすべての数字ですね。
実数というのは、3とか4などといったキリのいい整数と、2.9とか、8.6といった小数をあわせた数字のことです。
要は、塗ってるところ全部の数字と、想像してください。
ちょっと分かってきたでしょうか?
次はこの不等式に=のマークが加わったものを紹介します。
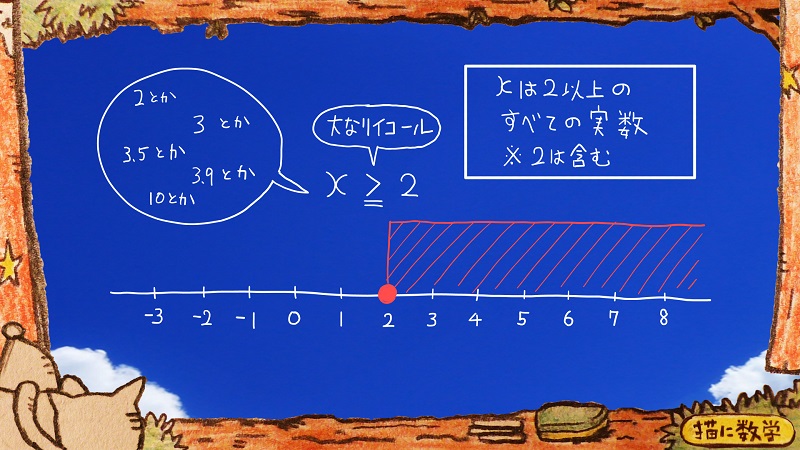
こちらですね。
≧←これは
先程の記号『大なり』にイコールが付いたもので
『大なりイコール』
と読みます。
先程は『xは2よりも大きいすべての実数』
だったのですが、これは
『xは2以上のすべての実数』
となります。
『2以上』は2を含みますので、数直線上の2のところはちゃんと塗りつぶしています。
このような違いがあるわけですね。

また、符号がひっくり返るとこのようになります。
≦←この符号は
小なりイコールと読みます。
『xは2以下のすべての実数』
となります。
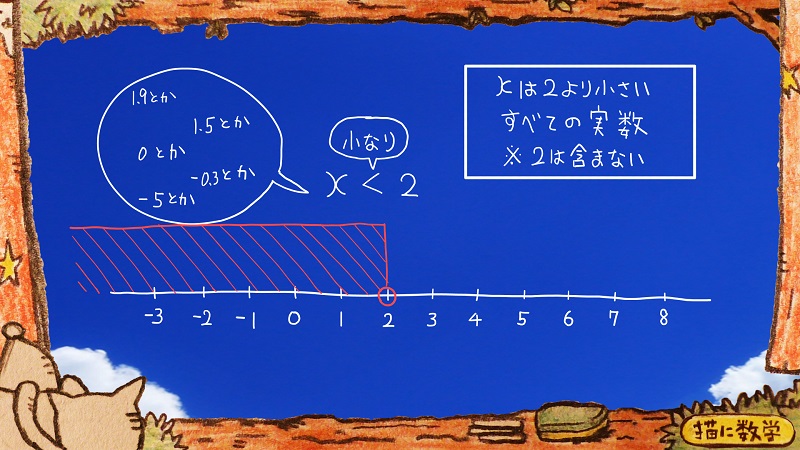
これに=がない場合はコレですね。
<←この不等号は
小なりと読みます。
『xは2よりも小さいすべての実数』
となって、この場合は2を含みません。
ちょっとこの式を使って、一次不等式の解き方(解くときの考え方)について、説明していこうと思います。
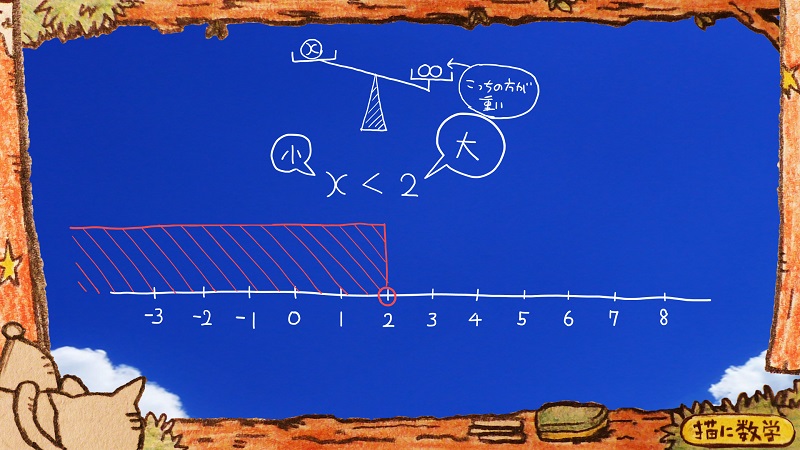
この不等式は
xと2を比べた時に、2の方が大きい値である。
という大小関係を表現しています。
もしもこの値が重さであるとするなら、このように、右側の天秤が下がるという状態になりますね。
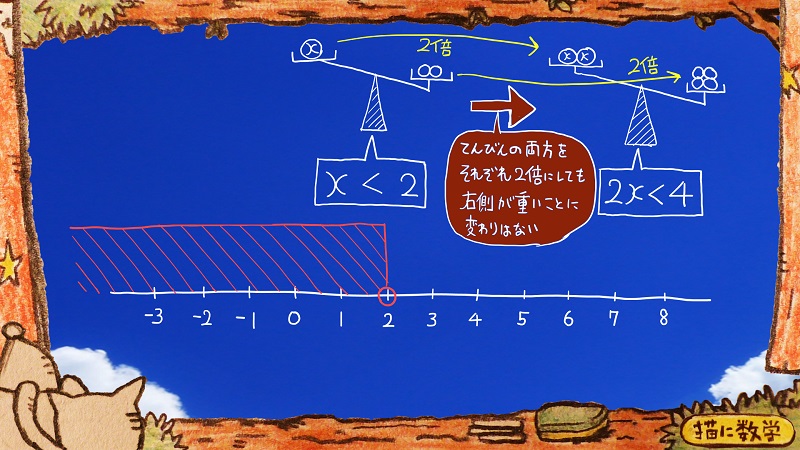
そして、この天秤の両方をそれぞれ2倍の重さにしたとしましょう。
xは2xに
2は4という具合に
それぞれ2倍にするとどうでしょうか。
天秤は相変わらず右側に傾いている状態ですよね?
軽いほうを2倍したものと
重いものを2倍にしたものを天秤にかけたら
重いものを2倍にしたもののほうが重いはずですよね。
2xと4の比較した結果を不等式で表すと
2x<4
ということになります。
ここまでは大丈夫でしょうか?
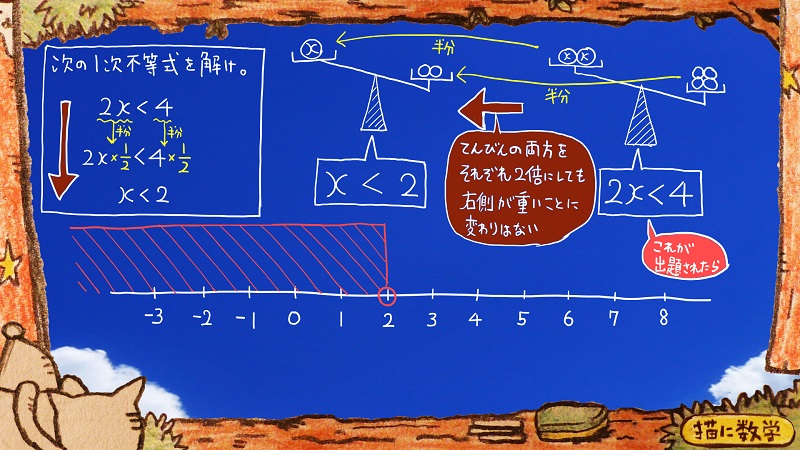
次にもしも、この
2x<4
が出題されて
この一次不等式を解け
という指示があったらどうでしょう?
この場合
今、説明したことを逆に考えていけばいいことになります。
左上の囲みの説明を見てください。
2xも4も
それぞれ半分づつにしたって
相変わらず
右側が大きな数字であることに変わりはないですよね。
なのでそれぞれを半分にすると、つまり\(×\frac{1}{2}\)すると
x<2
になります。
こうやって解答にたどりつくわけです。
不等式の解き方と考え方は、基本的にこのようになります。
では、もうちょっと複雑な形の不等式について
解く手順を見てみましょう。
一次不等式の解き方を天秤図で解説
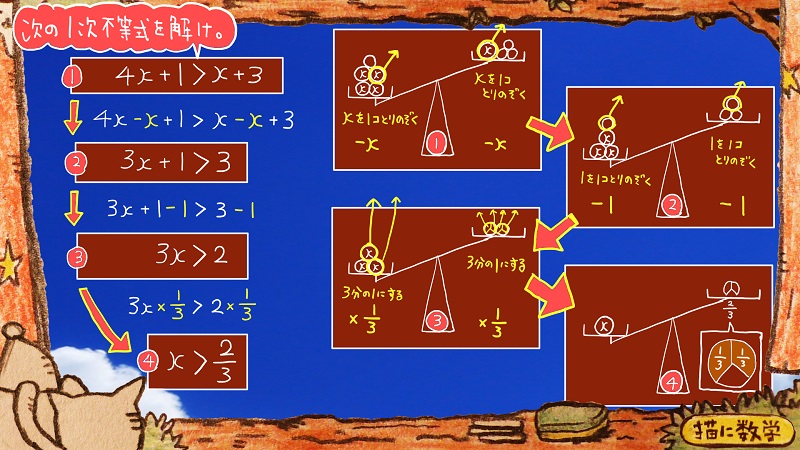
これですね。
4x+1>x+3
を解く問題です。
不等式を解いていく様子を天秤の図で説明したものも、右側に書いてあります。
最初の①の式から
②の式になるまでの操作ですが
不等式の右辺にあるxを消すことを考えて操作しています。
なので、天秤の両方からそれぞれxを1個ずつ取り除くという操作が書いてあるわけですね。
これで右辺にxがなくなりました。
不等式②の状態ですね。
次に左辺の3x+1の+1が邪魔だなということで両辺にそれぞれ-1をします。
これで不等式③ができました。
このように、基本的には
不等式の左辺にxだけの項
不等式の右辺には数字だけの項
にする、ということを考えて解いていくといいと思います。
次に
③の不等式
3x>2
ですが
この状態から最後の④にするには
右辺と左辺をそれぞれ3分の1にするといいですね。
両辺にそれぞれ×3分の1をすると
最後の④が導けて、不等式を解いたということになります。
この問題の解き方は以上になりますが、どうでしょうか?
次は不等式を解く場合に注意しなければいけないポイントについて説明します。
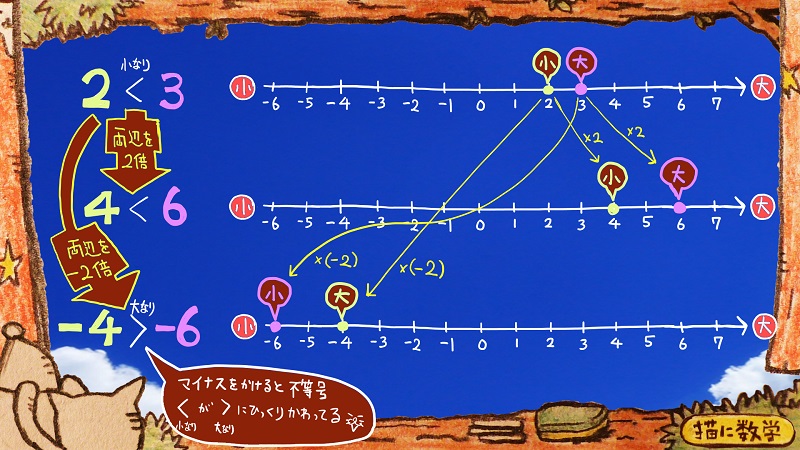
ごちゃごちゃ書いていますが
まず左上の
2<3
を見てください。
2と3を比べると3のほうが大きい
という大小関係を表現している不等式です。
右側の数直線上でも2と3が書かれています。
2よりも右側にある3のほうが大きい、ということが視覚的にわかりますよね。
さて、この2と3をそれぞれ2倍したとしましょう。
4と6になります。
数直線上で確認すると、その大小関係は
4よりも6のほうが右側にありますので、6のほうが大きいということがわかります。
不等式では
4<6
となります。
さっきの
2<3
の不等号の向きと変わっていませんよね。
ところが、この
2<3
の両辺に-2をかけるとどうでしょうか。
2は、-4に
3は、-6になりますよね。
これを数直線上で確認してみると
-6のよりも、-4のほうが右側にあるので、
-4のほうが大きい、ということがわかります。
数直線上では、右側にあるものほど大きい、ということですからね。
この大小関係を不等号で表現すると
-4>-6
というように
不等号の向きが
<
から
>
に変わっているのがわかりますね。
つまり、両辺にプラスをかけた場合は
不等号の向きはそのままだったのが
マイナスをかけた場合は
不等号の向きが逆になる
ということに気を付けないといけないワケです。
最初は慣れない方もいると思いますが
ちょっとこのあたり、問題を解きながら確認していきましょう。

二問あります。
①の問題は最初
両辺をマイナス1倍します。
不等号が逆向きになりますので
<を
>に変えて完了です。
②の問題はもうちょっと複雑な問題です。
最初の操作で
両辺を-1しています。
これは掛け算ではないので不等号の向きは変化しません。
天秤の両方に同じ量を
足したり引いたりしても
天秤の傾き具合は変わらなかったですよね?
つぎに
両辺にそれぞれ(マイナス2分の1)をかけています。
不等式の両辺にマイナスをかけているので
不等号の向きは逆向きになります。
≧が
≦になります。
このようにして解いていくわけです。
ちょっとわかってきたでしょうか?
つまり、不等式を解くときのポイントは、まとめるとこのようになります。

不等式を解くときに注意しなければいけないのは
不等号の向きが変わるときです。
それは、マイナスの値を
掛けたり、割ったりした場合だけに起こります。
それ以外は、方程式を解くときの要領でOKです。
マイナスの値を足したり引いたりしても
不等号の向きは変わりません。
このあたりは、習いより慣れろで、
教科書に載っている基本問題などの練習問題を、実際に手を動かして解いて、慣れるようにしてください。
以上、今回は一次不等式の解き方と考え方について解説しました。
不等式は、高校1年生の数学の教科書に掲載されている基本的な内容で、私立高校入試でもこの考え方は必要になります。
慣れるまで、最初はスピードよりも、丁寧に解くことを重視してくださいね。
ありがとうございました☆





