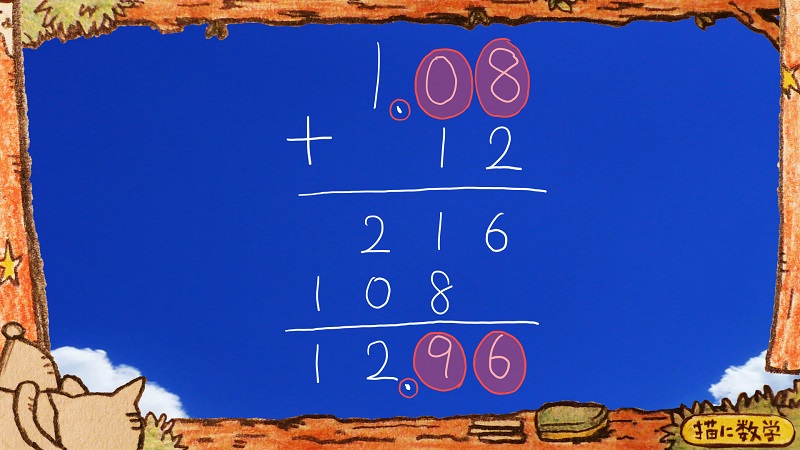数学でほぼ絶対の出題範囲は計算問題!沖縄県の公立高校入試

沖縄県の数学の最優先事項である計算問題を掲載しました。
沖縄県の公立高校入試対策として、ご利用ください☆
問題と解説をセットにしてご紹介します☆
| 沖縄県の公立高校入試数学~過去問2017年(平成29年)2017年(平成29年)の計算問題 |
| ① \(2-5×2\) |
| ② \(\frac{1}{5}÷(-\frac{3}{2})\) |
| ③ \(12×1.08\) (小数で答えなさい。) |
| ④ \(3\sqrt{2}+\sqrt{8}\) |
| ⑤ \((-3x)^2\) |
| ⑥ \((3x+2)-(x-4)\) |
続いて解説です☆
| 沖縄県の公立高校入試数学~過去問2017年(平成29年)2017年(平成29年)の計算問題 |
|
① \(2-5×2\)
四則演算を確認する計算問題です。 四則演算というのは+-×÷の4つの計算がまざった式を言います。 これには計算の順番があって、+-よりも×÷の方を先に計算しないといけません。 この問題で登場しているのは-と×なので、先に掛け算をしておかないといけない、ということです。 『5×2』を先に計算して『10』としておきます。 すると式は =2-10 となりました。 よって答えは =-8 となります。 |
|
② \(\frac{1}{5}÷(-\frac{3}{2})\)
分数の割り算の基本的な問題です。 『分数の割り算は、割り算のマークの後ろの分数の分母と分子をひっくり返す。そして、割り算のマークを掛け算のマークにする。』 ということを覚えておいてください。 どういうことかと言いますと 問題の式で具体的に説明すると、このようになります。 \(\frac{1}{5}÷(-\frac{3}{2})\) =\(\frac{1}{5}×(-\frac{2}{3})\) どうでしょうか? たしかに、『割り算のマークの後ろの分数の分母と分子をひっくり返って、割り算のマークが掛け算のマークに変わっている』ではありませんか? このようにして、分数の割り算が出題された場合、処理します。 結果、分数どうしの掛け算の問題になりました。 この場合先に答えの符号を出しておきます。 +かける-なので、答えの符号は-ですね。 あとは分数の分母どうしを掛けて、さらに分子どうしをかければ解答へとたどりつくことができます。 =\(-\frac{2}{15}\) これが解答です。 |
|
③ \(12×1.08\) (小数で答えなさい。)
小数の掛け算の問題です。 小数で答えないといけないので、このまま筆算で導きます。
よって答えは 12.96 になります。 |
|
④ \(3\sqrt{2}+\sqrt{8}\)
ルート8を変形します。 \(\sqrt{8}=\sqrt{2×2×2}=2\sqrt{2}\) なので \(3\sqrt{2}+\sqrt{8}\) は \(3\sqrt{2}+2\sqrt{2}\) となります。 ルートの部分が同じになりましたので、この二つの項は合わせることができます。 これを計算すると答えは \(5\sqrt{2}\) ですね。 |
|
⑤ \((-3x)^2\)
マイナス3を丸ごと2乗しますので (-3x)×(-3x)となり \(9x^2\)が答えとなります。 |
|
⑥ \((3x+2)-(x-4)\)
中学1年生で学習する、文字の登場する分配法則の手順の問題ですね。 \(-(x-4)\)の部分は(x-4)×(-1)という意味ですので 分配法則によって(カッコ)をはずすと -x+4 となります。 なので、 \((3x+2)-(x-4)\) =3x+2-x+4 =2x+6 となりますね。 |