小数や循環小数を分数に変換する方法をわかりやすく解説

今回は小数や循環小数を分数に変換する方法を解説します。

動画による授業をご覧いただいてもいいですし、それを板書した以下のページをご覧いただきながら勉強してもらっても大丈夫です。

できるだけわかりやすくまとめましたが、わからないポイントがあれば、YouTube動画のコメント欄にお知らせいただければ、可能な限り反映させていきます。

小数はわかるけど循環小数ってなに？

という方はこちらをご覧ください☆

(ウ)と(エ)と(オ)は、数字の上に小さな点がついていますね。

例えば(ウ)だったら、0.8の８の上に点があります。

これは１個しかついていないので、「８が繰り返される」という意味になって0.8の右に書いてあるような意味を表わしています。

たしかに８が繰り返されていますね。

(エ)の場合は、２の上にも５の上にも点がついていますね。

このように２個付いている場合は、二つの点の付いている数字とその間の数字が繰り返されるという意味になります。

この場合はご覧のように、２５２５２５…と「２５」が繰り返されることになります。

(オ)の場合は１と５に点がついていますので、その二つの数字に挟まれた２も含めて１２５が繰り返されるということになります。

これが循環小数です。

では、これら循環小数を分数に変換する方法を順番に説明していきます。

まず(ア)について解いてみましょう。

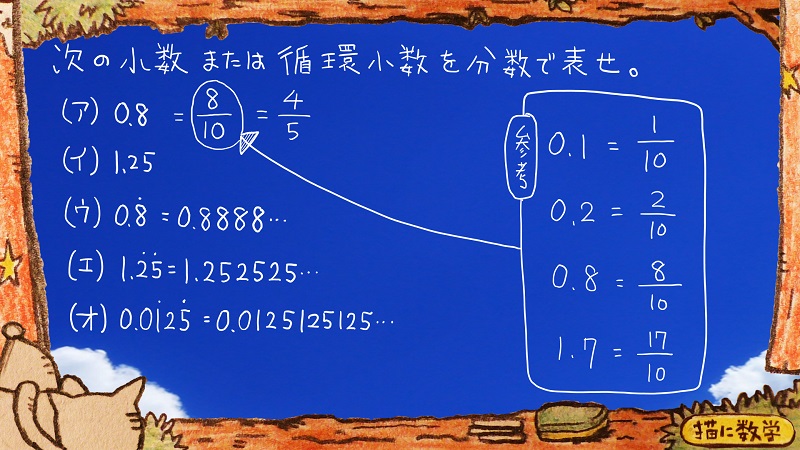
（ア）は中学生にとっては数学というよりも算数の復習になりますが、まずは「参考」と書いてある囲みを見てください。

0.1は１を１０で割ったもののうちの一つ分なので、分数で言うところの「１０分の１」と同じ分量になりますよね。

0.2だったらその0.1の２つ分なので、「１０分の１」の２つ分ということで「１０分の２」になりますよね。

その要領で考えていくと、結局0.8は、「１０分の８」だということがわかります。

約分して「５分の４」ですね。

どうでしょうか？

少し思い出してきたでしょうか？

続いて(イ)に進みます。

これは小数第二位という0.01の位まで数字が書かれているので、パッと答えが浮かばないときは、0.01って分数で表わすと何だったっけ？というところからまず考えます。

それが右の「参考」の部分ですね。

0.01は「100分の１」なので、

1.25は、それが１２５個あるわけですから「100分の125」ということになりますね。

最後にそれを約分して完了です。

さて、次はいよいよ循環小数を分数に直す方法をお話します。

ここから先の説明は中学数学で方程式を習っていないと、付いていくのは難しいと思いますので、ご注意ください。

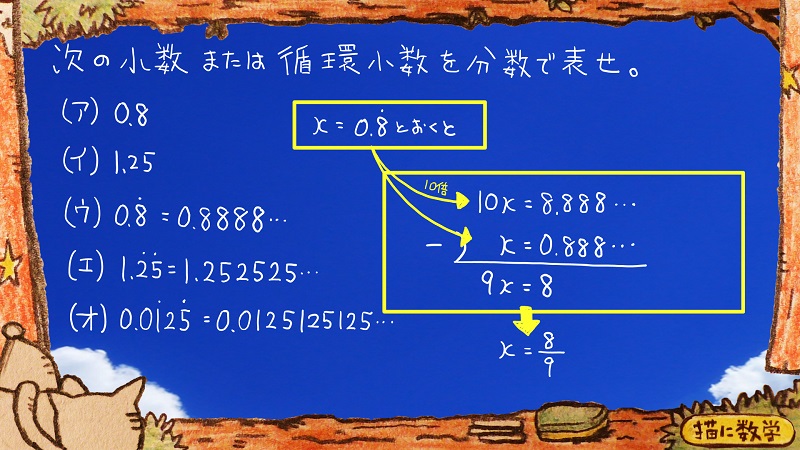
まず、（ウ）なのですが、問題になっている0.88888…をｘという文字に置き換えます。

そして、黄色の矢印のように、両辺を１０倍したものと、そのままのものを縦に並べて書きます。

そして、二つの式の左辺同士と右辺同士を引きます。

すると、ご覧のように右辺が８になってすっきりしましたね。

結局これは

９ｘ＝８ということがわかって、コレを解いて

ｘ＝９分の８という形になりました。

ｘは問題にあった循環小数そのものなので、９分の８が答えだということですね。

どうでしょうか？

たぶんこの説明だけでは、なにをしたのかわからなかったという方もいると思うので、次の(エ)を、もうちょっと丁寧に説明します。

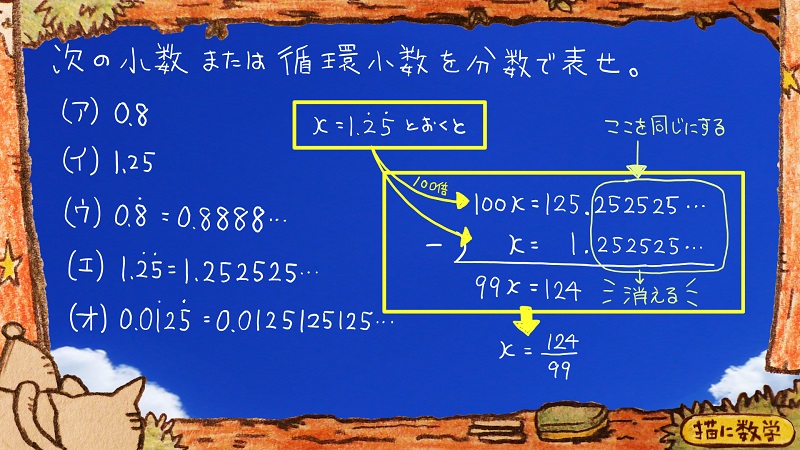
まずさっきと同じように、循環小数をｘと置きます。

それを黄色の矢印のように、両辺を１００倍したものと、そのままのものを、縦に２つ書き並べます。

すると、緑の囲みの部分が同じ２５２５２５…になっていますよね。

この状態で、左辺同士、右辺同士を引き算することで、緑の囲みの部分がきれいに消えてくれることになります。

なので、この段階で循環するという表現が消えてくれて、残った方程式を解くことでｘの値が求められるということになるワケです。

どうでしょうか？

ちょっとわかってきたのではないでしょうか？

では最後に(オ)の問題を解説して、小数を分数に直す問題を終りにしましょう。

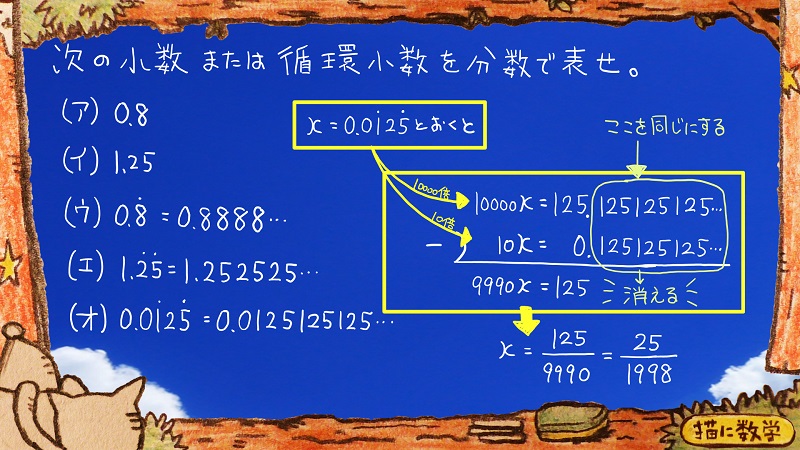
これもさっきと同様、問題の循環小数をｘと置きます。

そして、今度は両辺を１００００倍したものと、両辺を１０倍したものを準備します。

なぜ１０倍するのかというと、そうしないと緑の囲みの部分がきれいにそろってくれないからです。

ここがそろっていないと、引き算をしたときにきれいに消えてくれないですよね。

なのでこういった類の問題を解くコツは

・いかに循環している部分をそろえるか？

を意識することにあります。

なので、このように解くことも可能です。

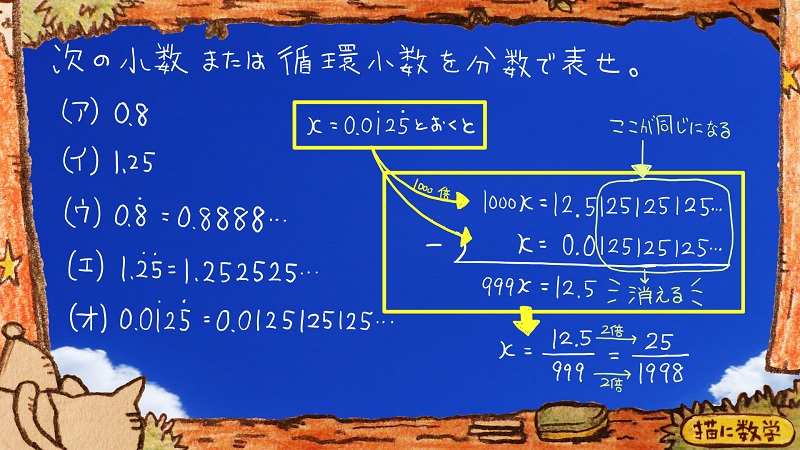
今度は一つ目の式を１０００倍、もうひとつの式はそのままにしていますね。

このやり方だと、小数第二位以下がきれいにそろうことになります。

この方法は、ｘについて求めたときに最初、分数のなかに小数が登場することになります。

まあちょっとだけややこしい形になっていますが、このやり方で分数の形を導いてもＯＫです。

以上、小数および循環小数を分数に変換する方法について解説しました。

慣れない場合は高校生だとチャートの例題など、実際の練習問題で手を動かしながら勉強してもらえればなと思います。