たすきがけ(数学)の因数分解で二次方程式を解く手順と方法~簡単な練習問題
前回は、このように中学生が教科書で習う二次方程式の解法パターンをまとめて解説しました。

因数分解をしたり、平方根の考えを使ったり、解の公式を使ったりと、いろいろな解き方がありましたね。
今回は、この表にプラスして、たすきがけという因数分解の方法とコツをお話します。
たすきがけによる因数分解は、主に高校数学でよく使うことになるので、必要な方はご覧いただければと思います。
以下はこの授業動画の板書になります☆
※また、YouTube動画で授業をご覧になる場合は設定により再生速度を調節できます。
たすきがけによる因数分解の手順と方法
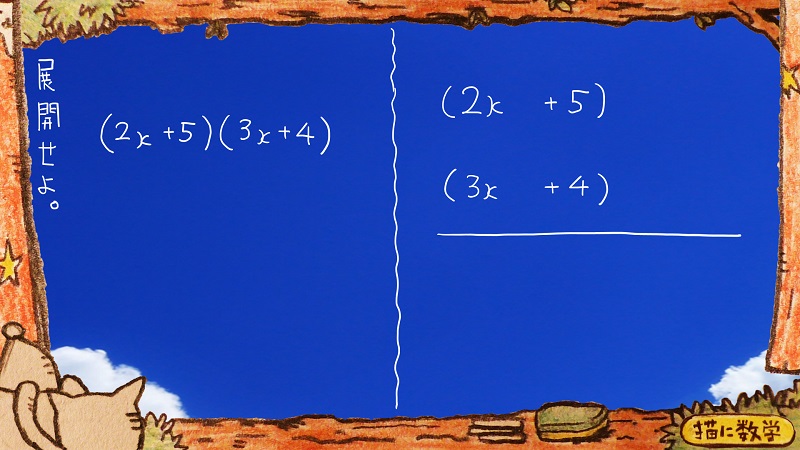
最初にまず、たすきがけの方法がどうやってつくられているのかのお話もしようと思います。
「展開せよ」という指示がありますが、いまご覧いただいている式のかたちはもう、因数分解された形になっています。
右半分は、左半分の式と同じ二つの因数が、たてに並べられたものだと思ってください。
さてこれから、この因数分解された式を分配法則によって展開していきます。
かけていく順番が違っていても、最終的に現れる展開された式に違いはないので、今回のテーマに合う順番で展開していきます。
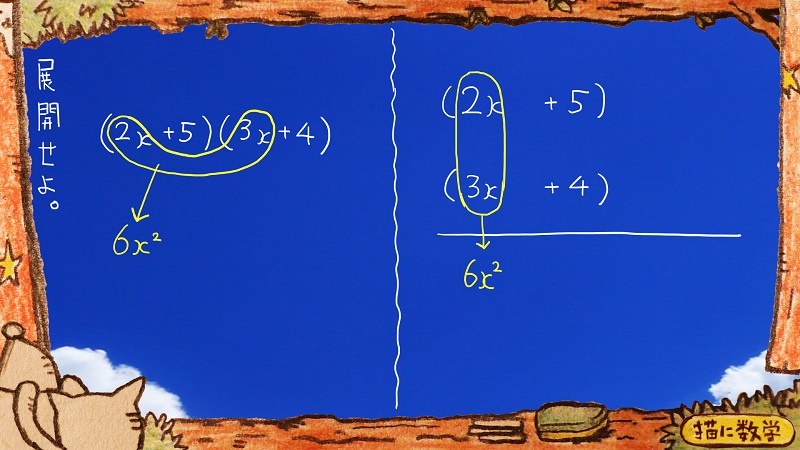
まず2xと3xをかけます。
6xの2乗が登場しますね。
右側の式では6xの2乗をこのように書いておきます。
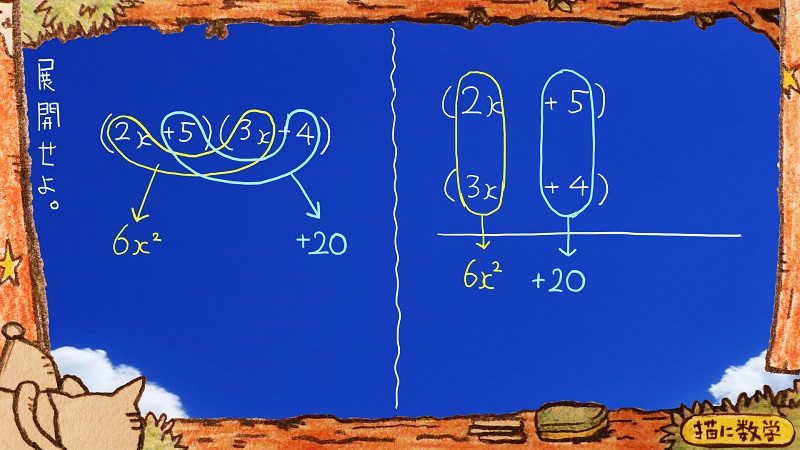
つづいて
5と4を掛けあわせます。
ご覧のように+20が現れましたね。
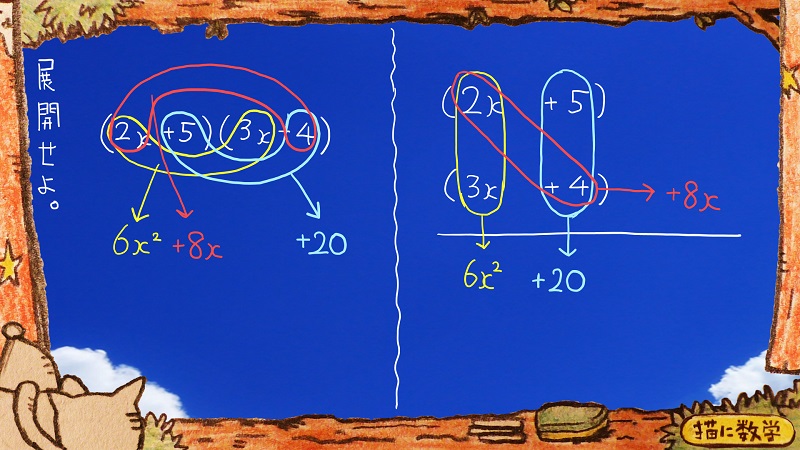
次に2xと4を掛けます。
8xが登場しました。
右側の式ではちょっとややこしいですが、このように、ななめの位置関係にある二つの数字を掛け合わせたことになります。
8xは、もう下には掛けないので、右側に書いておきます。
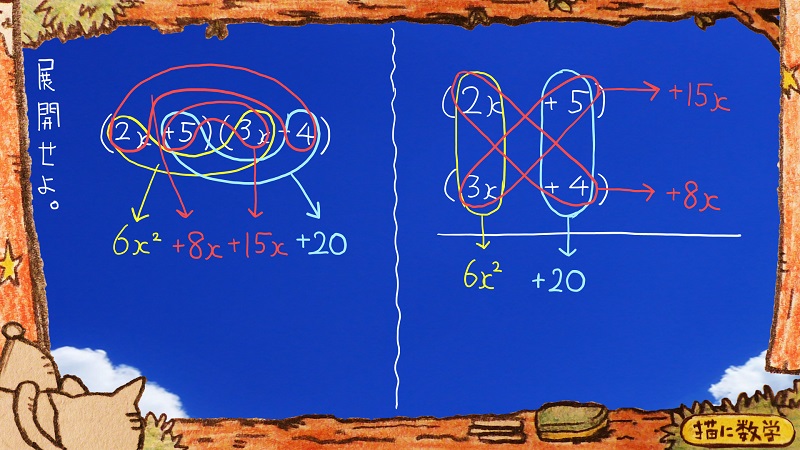
最後に5と3xを掛け合わせます。
15xが登場しました。
右側の図でも、さっきと同じようにななめにかけわせて、結果の15xを右側に書いておきましょう。
さて、あともう一息です。
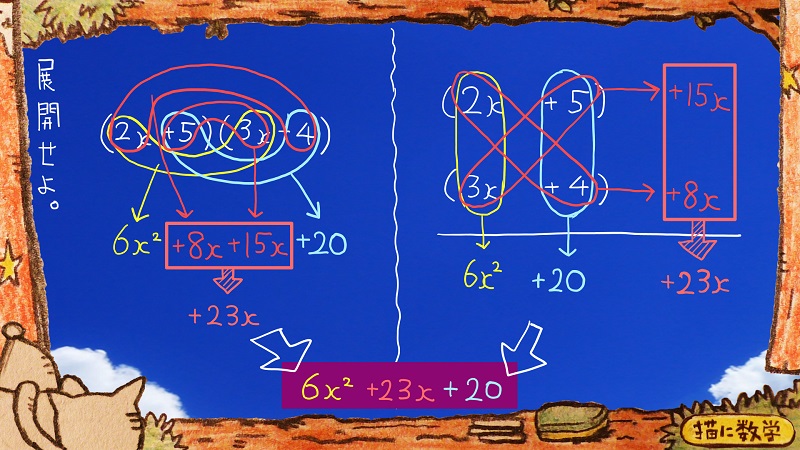
8xと15xは、まとめることができるので、23xにまとめておきましょう。
右側の図ではその値を下の方に書いておきます。
さて、これで2通りの表現で、展開することができました。
きれいに書き直すと、両方とも、中央に下にあるようになりますね。
これで展開は完了したワケですが、さて、この一番下の式を最初の因数分解された形に直すには、どうすればいいでしょうか?
そこで右側で書いていた図が活躍します。
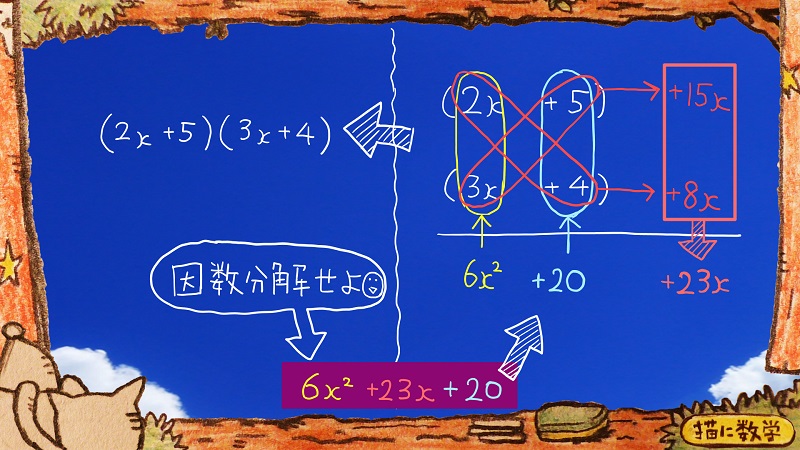
右側で展開していった手順をさかのぼっていったら因数分解された形にもどせるゾというのが、今回お話する「たすきがけの考え方」です。
一番下の式を因数分解せよ、という問題があったとしましょう。
今度はこの画面を見ながら手順を説明していきますね。
まず、xの2乗の項が先頭だということは変わりませんが、あとの並びを入れ替えて書きます。
先頭から、黄色、水色、赤色の順に書き出します。
それから、先頭の黄色の項を因数分解します。
6xの2乗を2xと3xに分解しますね。
ほかにもいろいろな分解のパターンがあるかと思います。
たとえば、xと6xにわけるとか
-2xと-3xにわけるとか、ですね。
ただ、あとで説明しますが、この場合はこの分け方がふさわしいです。
それから水色で書かれた+20の項を見ます。
この20を、5と4という2つの因数に分解していますね。
これもまた、ほかにもいろいろな分解のパターンがありますが、結局そのペアがふさわしいということが、あとでわかります。
さて、それぞれ分解したこのペアの因数を、赤色でしめしたように、かすきをかけるようにして、それぞれ掛け算をします。
すると、右側にその結果が並びますね。
15xと8xがそれにあたるのですが、こんどはその数字をたします。
ちょうど、最初に書いてあった23xとぴったり一致しましたね。
ここが重要なところなのですが、ここでちょうどぴったり23xと同じにならなければ、たすきがけによる因数分解は失敗、ということになります。
さっき6xの2乗を分解するパターンが2xと3x以外にも、いろいろあるけど結局これしか出来ない、みたいなことを言いましたね。
本当は-2xと-3xに分解しても、20を分解するときにつじつまを合わられる組み合わせがあるのですが、それでも一応答えにはなります。
ちょっとこのあたり、次の練習問題でお話しますね。
まあ結局は、最終的に赤色の23xの部分でつじつまが合わないといけないということです。
つじつまが合った場合のみ
(2x+5)と(3x+4)を取り出して因数分解完了!というように導くことができます。
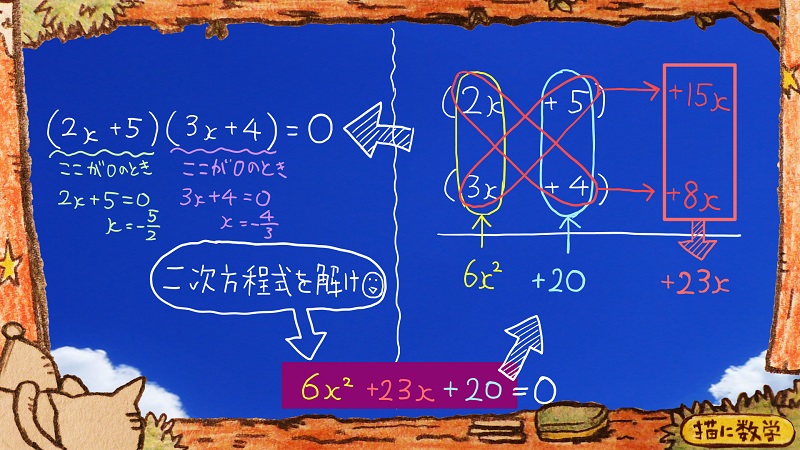
ちなみにこのように二次方程式の問題になっているときも、たすきがけによる因数分解をしてからxを求めます。
因数分解したあとに「ここが0のとき」という書き込みがありますが、このあたりの説明はこちら↓の解説が詳しいので、ちょっとわからないという方はご覧ください。
⇒中学数学で習う因数分解を使った二次方程式の解法パターンまとめ
それではこれから、簡単な練習問題と、定期テストに出るレベルの問題を解いて、たすきがけを身につけていきましょう。
あと、たすきがけの筆算みたいなかたちのなかには、xの2乗やxを書かないで(つまり数字だけを書いて)教科書なんかでも説明されています。
やっている内容は同じなのですが、ここではわかりやすさを優先してこの表記で進めようと思います。
たすきがけ(数学)の簡単な練習問題~教科書レベル
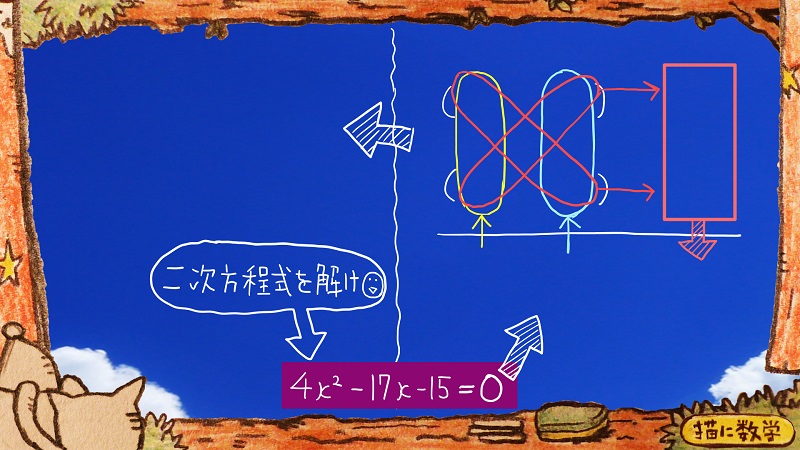
どうでしょうか?
一度紙とペンを使って、実際に手を動かして解いてみてください。
続いて解答を表示します。
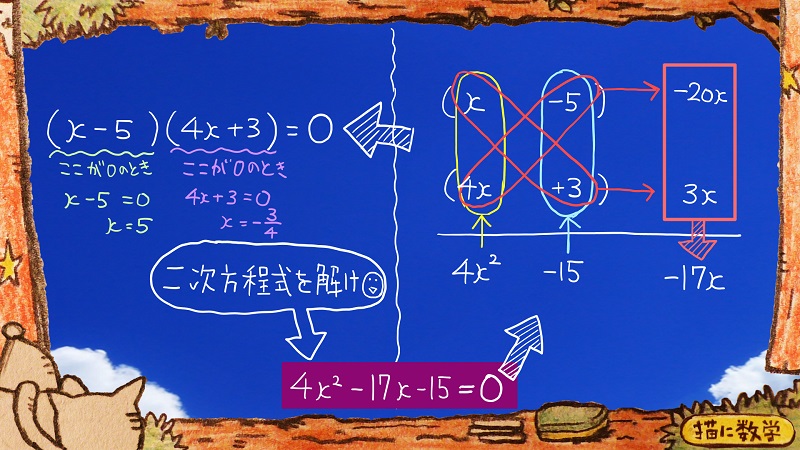
いかができたでしょうか?
このようになりましたでしょうか?
たぶん、これとは違う因数分解のかたちになった方もいると思います。
それがこれですね。
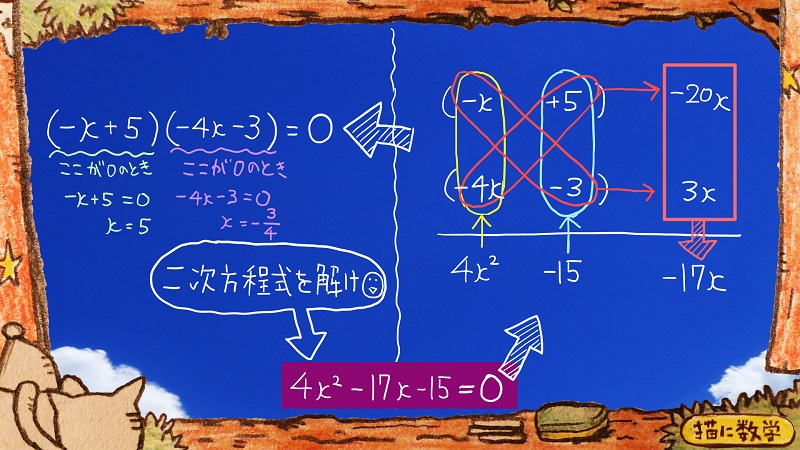
この場合だと
4xの2乗を-xと-4xにわけるというところが難しかったかもしれませんね。
※たすきがけでこの形に因数分解できない場合でも、別に問題はありません。
マイナスかけるマイナスはプラスになるので、この分解のパターンもあるということですね。
これでも解を導き出せるのですが、さっきのかたちはxのまえに-がついていないぶん、すっきりしていますね。
もしも教科書にこの問題が例題としてあった場合、おそらくさっきの因数分解の形が掲載されていると思います。
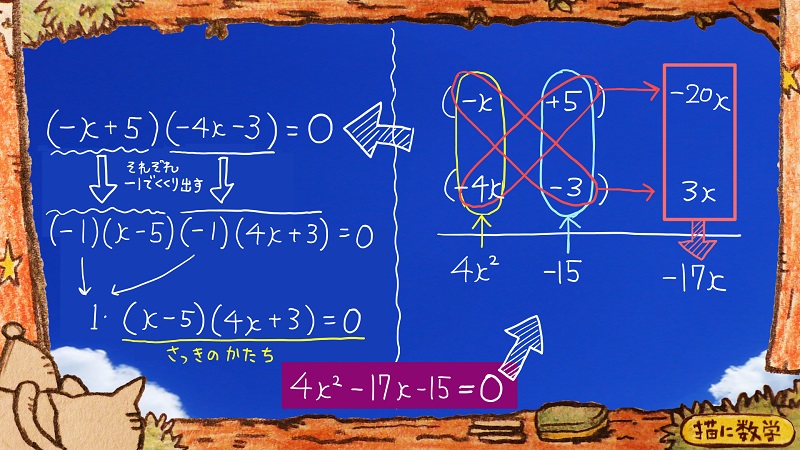
これを変形していくと、さっきのかたちと同じ結果が出ていたということがわかるかと思います。
(-x+5)も(-4x-3)もそれぞれ-1でくくり出します。
くくりだした(-1)同士を掛け合わせると1になって、1という表記を省略することができますよね。
それがすなわちさっきの形になっているということです。
それでは次の問題に移ってみましょう。
たすきがけ(数学)の簡単な練習問題~定期テスト対策レベル

これはちょっとややこしい形でしていますね。
高校数学の定期テストに出そうな問題ですが、さっぱりわからないという方はまず解答を見てください。その後で実際に手を動かして解くことでパターンに慣れてほしいと思います。

けっこうごちゃごちゃしていますが、これが因数分解の手順ですね。
これまでと違うのが文字がxとyの2種類あるという点です。
このようなとき、もしも解法の道筋が見えなかった場合は、一つの文字について、降べきの順に整理します。
降べきの順にっていうのは白い囲みに書いてあるように
なんとかxの2乗
なんとかx
なんとか
というようにxの次数の大きいものから小さいものに順に並べていくということです。
できれば一番次数の小さい文字について整理したほうが、一般的にはその後の解法の見通しがよくなります。
どういうことかと言うと、この場合はxもyも2乗まで登場していますね。
これが、例えばxだけ3乗まで登場していたとしましょう。
その場合、yは2乗までなので、xの次数よりも、yの次数のほうが小さいと判断します。
なのでその時はyについて、降べきの順に整理する、ということになります。
この場合はxもyもどちらも同じ次数なので、まあどちらでもよさそうですが、とりあえずxについて降べきの順に整理して説明していきます。
降べきの順に整理すると、xのついていない項が最後にずらりと並びますね。
この部分が因数分解できそうなので、たすきがけを使います。
最後に紫色で「たすきがけ」と書かれた工程があるのですが、ここが一番難しいと思います。
これもたすきがけによって式全体を因数分解できるのですが、どうでしょうか?
むらさきの箱のなかの説明がわかりますでしょうか?
理解しにくいのが
(y-3)(2y+5)の部分だと思います。
ここがたとえば単に6と書かれていた場合
2と3にわけたりしますよね?
そしてこの部分はすでに
(y-3)と(2y+5)という掛け算でつながった形で書かれているので
(y-3)と(2y+5)とにわけることができるというわけです。
このわけ方で、最終的に(3y+2)xの部分において、つじつまが合うので、これで因数分解ができる、ということになります。
いかがでしょうか?
ややこしいと感じた方は、このむららきの工程だけ何度か手を動かして慣れてから、全体を解くことをおすすめします。
以上、これでたすきがけを利用した因数分解の方法の説明を終わります。





