必要条件と十分条件の違いについて覚え方のコツを解説します。

題材：必要条件と十分条件の意味の違い	難易度：★☆☆☆☆☆☆☆☆☆

今回は、高校数学の（主に数Ⅰの「論理と集合」で学ぶ）必要条件と十分条件の違いと覚え方のコツについて、わかりやすく解説していきます。

高校１年生で学ぶ数学（数Ⅰ：命題と条件）の、まぎらわしいポイントの代表みたいなテーマです。

なのでベン図も使って、できるだけわかりやすく解説していきます。

まず、この例題を見てください。

コレは、空欄のなかに入るのは①から④のどれか？という問題です。

ポチが犬であること

と

ポチが動物であること

が

お互いにどのような条件になっているかを聞いているのですが

そもそも答えの選択肢にある言葉の意味がわからないという方もいると思います。

１：必要条件であるが、十分条件ではない

２：十分条件であるが、必要条件ではない

３：必要十分条件である

４：必要条件でも、十分条件でもない

と、４つ選択肢がありますね。

なので、この問題では、このまぎらわしい言葉の違いを理解して、そのニュアンスをつかんでもらえればと思います。

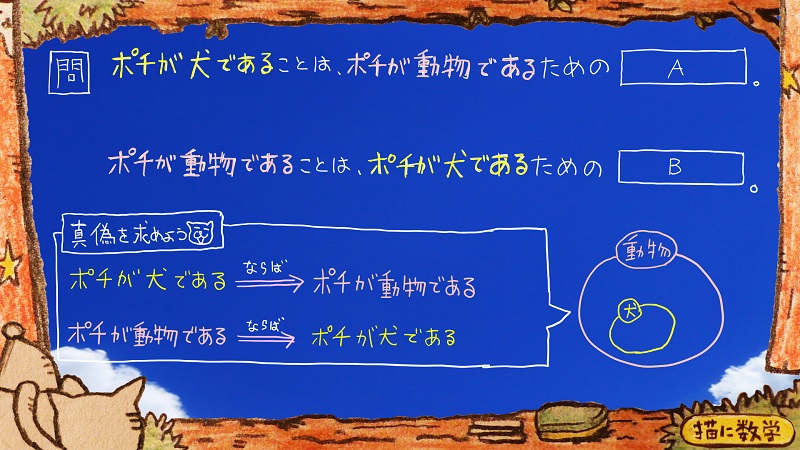
まず、この図のように、ふたつの命題を用意して、その真偽を確かめます。

命題が、常に正しく成り立つのであれば真を

命題が、常に成り立たない反例が見つかるのであれば偽だと見なします。

たとえば、この最初の命題ですが

「ポチが犬であるならば、ポチは動物である」

はどうでしょうか？

ポチが犬でありさえすれば、それで十分、ポチは動物と言えます。

なので「この命題は真である」ということが判別できました。

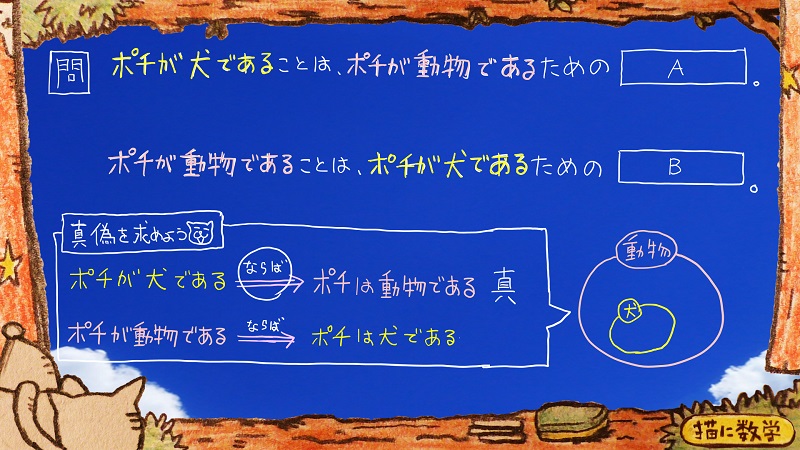
では

「ポチが動物であるならば、ポチは犬である」

はどうでしょうか？

ポチが動物であるからと言って、それが必ずしも犬である、ということにはならないですよね。

たとえばポチが猫であったとしても、「ポチは動物である」ということは言えてしまうワケですから。

つまり、「ポチが猫である」という反例があげられることになるので

「この命題は偽である」ということがわかります。

これで二つの命題の真偽を確かめたことになりますが

ここでちょっと右のベン図を見てください。

ふたつの円の包含関係はこのようになっていますね。

さっき

「ポチが犬であるならばポチは動物である」という命題は真だと解答しました。

この図の黄色の部分が「ポチは犬である」という条件を満たす範囲です。

ポチは柴犬かもわからないですし

ポチはチワワかもしれません。

まあ、ともかくポチは犬なわけです。

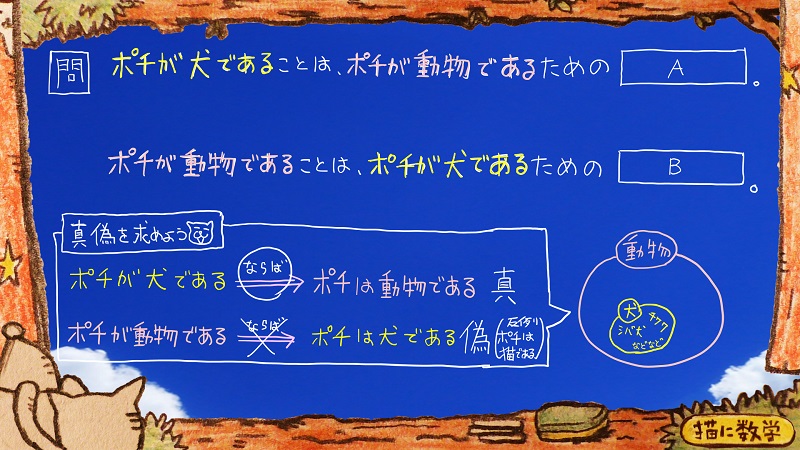
そしてこの黄色の円のなかであれば「動物である」という円のなかにも絶対に入っているということになりますよね。

つまり「ポチが犬である」ということがわかっていれば、それで十分、「ポチが動物である
」ということが言えてしまうのです。

なので、最初の問題の文章をあらためて解釈すると

・ポチが犬でありさえすれば、それでもう十分「ポチは動物である」と言えてしまう。

となります。

なので、これは十分な条件ということで「十分条件」なわけです。

ただ「ポチが動物である」ためには、なにも「ポチが犬である」必要はありませんよね。

たとえばポチが猫であったとしても「ポチが動物である」ということが言えるわけですから。

なので空欄Ａには「十分条件であるが必要条件ではない」という答えが入るわけです。

つづいて空欄Ｂを考えてみましょう。

さっき

・「ポチが動物である」ならば「ポチは犬である」

という命題の真偽を確かめたら「偽」ということがわかりましたね。

ポチが動物であるからと言って、ポチが犬であるとは限らないじゃないか。

猫かも知れないじゃないか。

という反例を出したと思います。

これをもう一度、右のベン図で確認してみましょう。

「ポチが動物である」という大きい方の円の条件を満たしたからといって、それが必ず黄色の円のなかの「ポチが犬である」という条件をも満たすとは限らないですよね。

反例で「ポチが猫である」というのを指摘したのもそういうことです。

これは言い換えれば、

「ポチが動物である」ということだけではまだ、「ポチが犬である」ためには不十分な条件ですよね。

だけど少なくとも「動物である」ということは「犬である」ためには必要な条件ですね。

今のをもう一度、もうちょっと短く言いますね。

「ポチが動物である」という条件は「ポチが犬である」ために必要な条件ではあるが、それだけじゃ不十分、ということですね。

なので、空欄Ｂには

必要条件であるが、十分条件ではない。

という選択肢が入ります。

必要条件と十分条件の用語の意味はわかりましたか？

これでまあ、用語の使い方を少し理解していただけたかと思います。

ただ、この問題のように、具体的なイメージがしやすいお題であれば、その意味を考えながら解答することは比較的簡単なのですが、たとえばこれが数式の登場するお題であったら、意味を考えはじめるとワケがわからなくなってしまいます。

なので、今度はｘの数式が登場する問題を解いてみましよう。

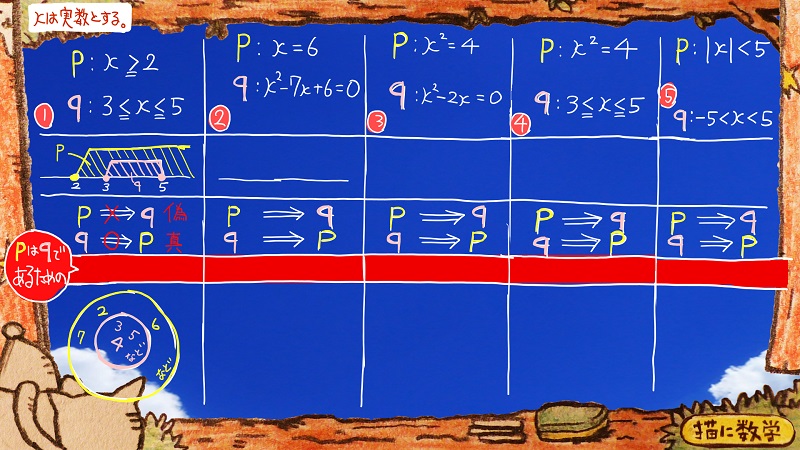
これですね。

さっきの例題と照らし合わせて、機械的に解答する手順で解いていきます。

意味を考えながら答えようとすると、ややこしくなる人もいると思います。

なので、最後に覚えかたの参考になる語呂合わせみたいなものもご紹介します。

また、さっきの問題で活躍しなかった残りの２つの選択肢

・必要十分条件である

・必要条件でも、十分条件でもない

ですね。

それらも問題に登場させていますので、解答できるようにしていきます。

上の例題は、問題文を省略していますが、たずねられていることは、赤色のスペースに入る文面をさっきの選択肢のなかから考えよう、という問題です。

ｐはｑであるための必要条件なのか十分条件なのか、とかそういったことですね。

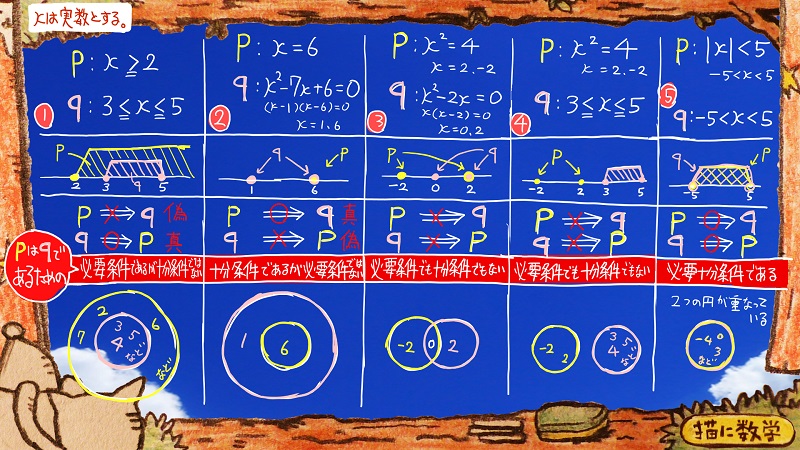
まず、①の問題を見てみます。

一番上の段には、ｐとｑとそれぞれにｘの登場する方程式が書いてあります。

このｘはさっきの話で言う「ポチ」にあたります。

ｐにもｑにも、それぞれｘの範囲が定義されてありますが、この定義の幅こそが

さっきの話における、ポチの定義の幅に対応しています。

ちょっと表の下のほうを見てましょう。

ｐとｑの関係を整理するためにいろいろ書いてありますね。

表の上から２段目は、ｐとｑの関係が数直線状に図示されています。

一番下にベン図でも表現されていますが、結局ここで明らかにしたいことはｐとｑのどっちがどっちを包み込んでいるか、という包含関係です。

さっきの例題も「ポチは犬である」と「ポチは動物である」の包含関係を把握することが解答に役立ったと思います。

この情報だけで解答できる人もいるとは思いますが、

ｐならばｑ

と

ｑならばｐ

の真偽も確認しておきます。

黄色であるｐのゾーンは、なかのｑのゾーンをすっぽり包んでいるので、さっきの話でいうところの「ポチは動物である」にあたります。

なので、

ｐならばｑ

というのは

「ポチが動物である」ならば「ポチは犬である」の真偽と一致することになりますね。

動物であるからと言ってそれが犬であるとは限らないので、偽となります。

逆に

ｑならばｐ

というのは

「ポチが犬である」ならば「ポチは動物である」の真偽と一致しますね。

犬でありさえすればそれでだけでもう動物なので、真となります。

さて、それじゃあ赤い部分の解答欄にはどんな文面が入るのでしょうか？

「ｐはｑであるための」とありますから

・「ポチが動物である」ことは「ポチが犬である」ための○○○○？

という問題と答えは同じことになります。

「ポチが動物である」という条件は、たしかに「ポチが犬である」ためには必要な条件だけども、それだけじゃ不十分な条件、でしたね。

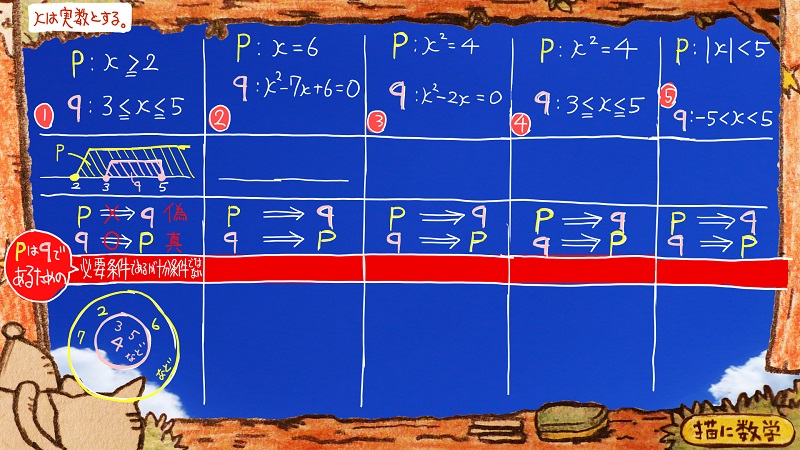
なので、①の答えは「必要条件であるが十分条件ではない」になります。

つづいて②に行きます。

②のｐはｘ＝６になっています。

ｑは、二次方程式になっていますが、ｘを求めると

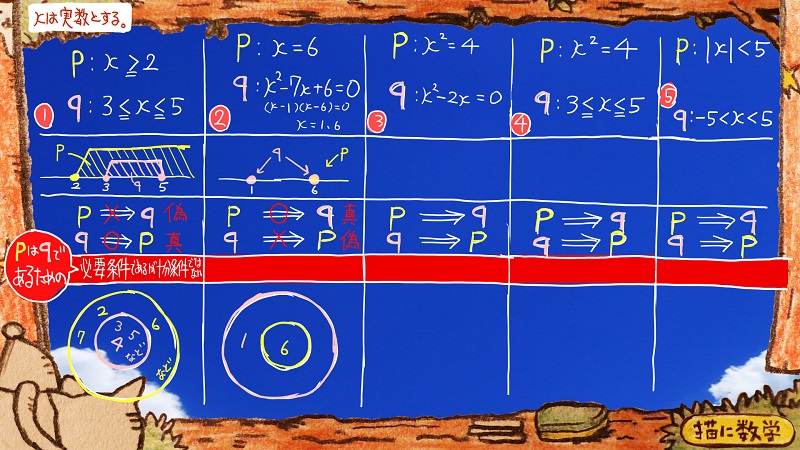
ｘは１と６になります。

ｐとｑの包含関係が①の問題とは逆になっていまね。

そして、その真偽をそれぞれ確かめてみると、さっきとは反対の結果が出ることになります。

下のベン図をみると、ｐでありさえすれば、その条件だけで十分ｑになっている。

ので

ｐはｑであるための

「十分条件であるが必要条件ではない」

ということがわかります。

この①と②の違いがややこしいと思いますので、覚え方も最後に紹介します。

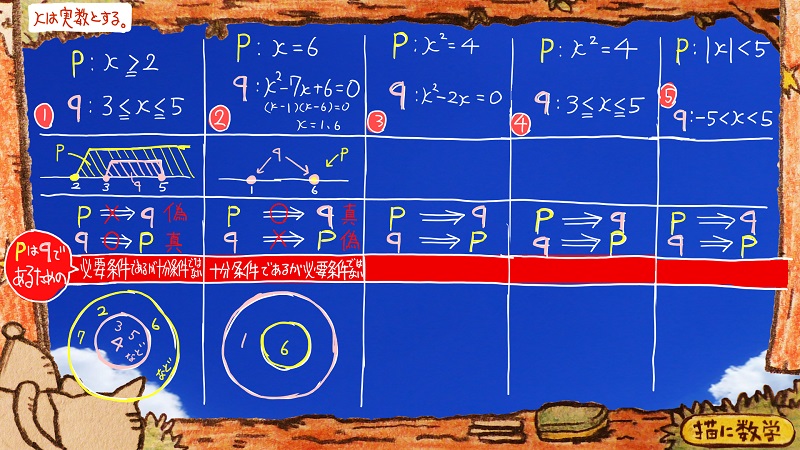
続いて③④⑤を一気に見ていきましょう。

「必要十分条件」と「必要条件でも十分条件でもない」問題のパターン

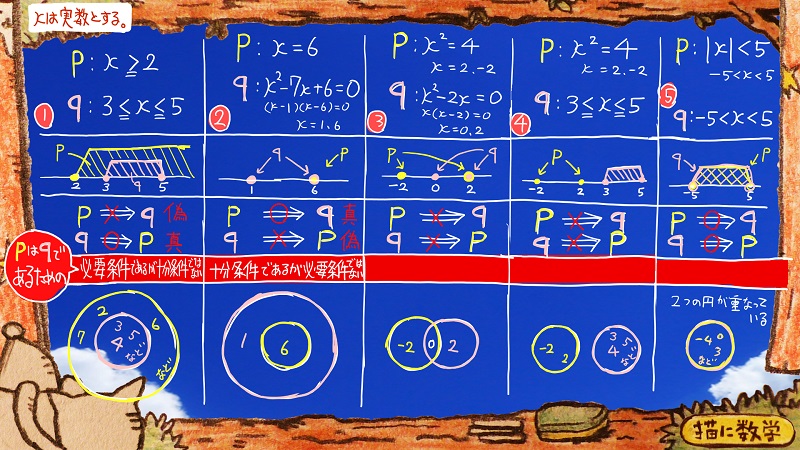
答え以外の部分はこんなふうになっています。

③と④の問題のベン図を見ると、

①、②の問題のように、

ｐとｑのどちらかがどちらかをつつみこんでいる

という関係図ではないですよね。

真偽を調べてみると

ｐならばｑも

ｑならばｐも

どちらも常に成り立つわけではない「偽」であることがわかります。

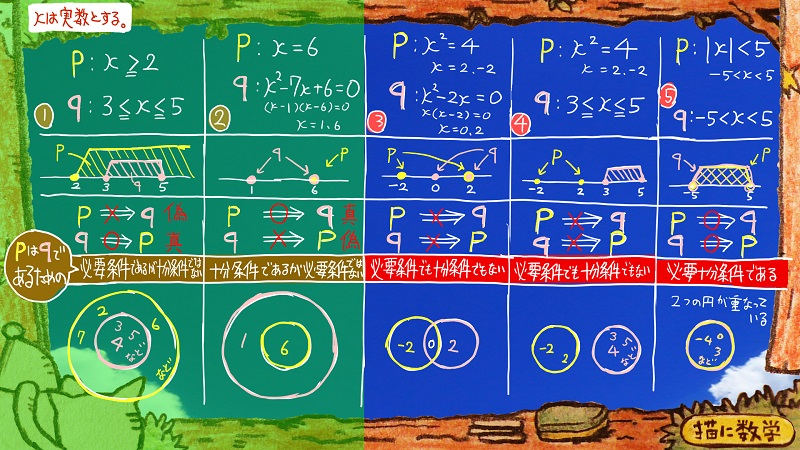
この場合は

ｐはｑであるための「必要条件でも十分条件でもない」

という解答になります。

また、⑤の問題のベン図は、ｐの円もｑの円もちょうどぴったり重なりあっています。

真か偽かを調べてみると

ｐならばｑも

ｑならばｐも

どちらも成立するので「真」ということになります。

こんな場合は

ｐはｑであるための「必要十分条件である」

という解答になります。

このような問題は真か偽かを確かめて、

両方とも「偽」であれば

「必要条件でも十分条件でもない」

と答えればいいですし。

両方とも「真」であれば

「必要十分条件である」

と答えればいいです。

また、問題文の前置きに「ｐはｑであるための」

とありますが、これが

「ｑはｐであるための」

というようにひっくり返っても、答えはそのまま変わらないですね。

けれど①と②の問題は

「ｑはｐであるための」

というようにｐとｑがひっくり返ったら

①の答えと②の答えが入れ替わるように変わってしまいます。

つまり

①は

・ｑはｐであるための十分条件であるが必要条件ではない

になりますし

②は

・ｑはｐであるための必要条件であるが十分条件ではない

というようになります。

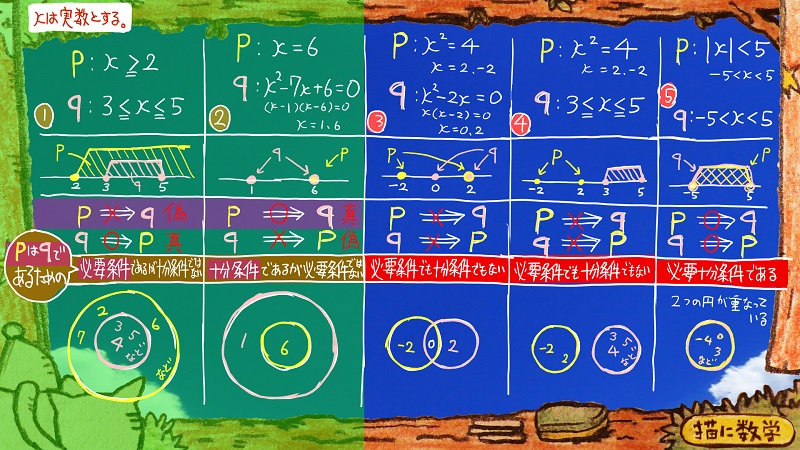
なので、真偽の確認と同時に、この順番も一緒に確認して答えないといけないということですね。

必要条件、十分条件の覚え方のコツ

①と②の解答の手順と覚え方なんですが

まず

真偽を確認して

一方の命題が真で、もう一方の命題が偽だということが前提となります。

両方とも真であったり、両方とも偽であったりしたら問題③、④、⑤のパターンということになりますよね。

で、真か偽かを確認したら問題文を確認します。

「ｐはｑであるための…」という聞きかたをしていますので

その順番の並びになっている

「ｐならばｑ」という命題の真偽を見ます。

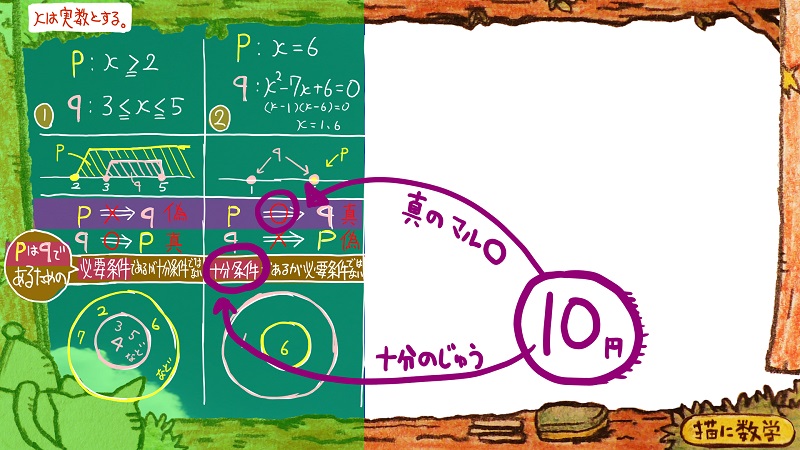
ちょっと②の問題から話していきますね。

②の問題ではそれが真となっていますよね。

この真である、という意味を表わした○のマークと連想させて僕は解答しています。

実際には、ここに○を書いたり×を書いたりしないんですが

「ならば」が成立するという意味で、わかりやすいように○を書いています。

この○のマークと十分条件ということが結びつけて覚えることができればいいので

僕はこのように、１０円玉の絵で覚えています。

１０円玉の丸い形がそのまま「真」を表わす○のマークです。

で、十円の十が十分条件の十ということで、語呂合わせ的に連想できるようにしています。

紛らわしいものが二つあってそれを覚えるときは、片方をしっかりこのように覚えておけば、結構楽に使い分けることができます。

もう一方のほうは、「それ以外の時」というように覚えることもできるからです。

けれど、一応念のために

①の問題のパターンも覚え方をお話しておきます。

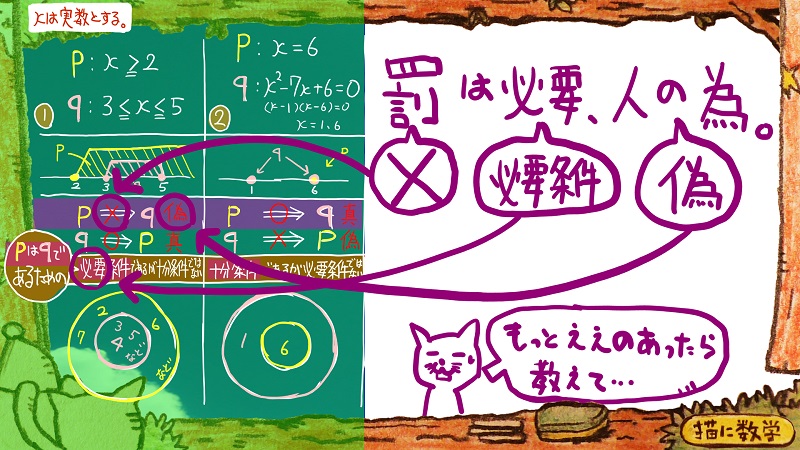
①の問題は、○ではなくて×なので、×のマークと必要条件という言葉を結びつける必要があります。

なので

「罰は必要、人の為」

と覚えます。

罰はバッテンマークのバツですね。

必要は、必要条件の必要です。

最後の人の為は

「偽」という漢字を右の部分と左の部分とに分けると「人」という字と「為」という字がでてきますよね。

これで語呂合わせのようにして覚えてもらえたらと思います。

いかがでしたでしょうか？

今回は必要条件と十分条件の使い方と覚え方について解説しました☆